Lesson 11Using an Algorithm to Divide Fractions
Let’s divide fractions using the rule we learned.
Learning Targets:
- I can describe and apply a rule to divide numbers by any fraction.
11.1 Multiplying Fractions
Evaluate each expression.
11.2 Dividing a Fraction by a Fraction
Work with a partner. One person should work on the questions labeled “Partner A,” and the other should work on those labeled “Partner B.”
-
Partner A.
Find the value of each expression, and answer the question by completing the diagram that has been started for you. Show your reasoning.
-
How many s in ?
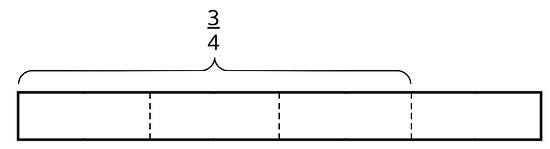
-
How many s in ?
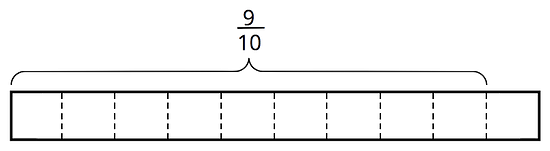
Use the applet to confirm your answers and explore your own examples.
-
-
Partner B.
Elena said: “If you want to divide 4 by , you can multiply 4 by 5, then divide it by 2 or multiply it by .”
Find the value of each expression using the strategy that Elena described.
Pause here for a discussion with your partner.
-
-
Complete this statement based on your observations:
To divide a number by a fraction , we can multiply by ________ and then divide the product by ________.
-
Select all equations that represent the statement you completed.
11.3 Using an Algorithm to Divide Fractions
-
Calculate each quotient using your preferred strategy. Show your work and be prepared to explain your strategy.
-
- After biking miles, Jada has traveled of the length of her trip. How long (in miles) is the entire length of her trip? Write an equation to represent the situation, and find the answer using your preferred strategy.
Are you ready for more?
Lesson 11 Summary
The division is equivalent to , so we can think of it as meaning “ of what number is ?” and represent it with a diagram as shown. The length of the entire diagram represents the unknown number.
If of a number is , then to find the number, we can first divide by 3 to find of the number. Then we multiply the result by 4 to find the number.
The steps above can be written as: . Dividing by 3 is the same as multiplying by , so we can also write the steps as: .
In other words: . And , so we can say that:
In general, dividing a number by a fraction is the same as multiplying the number by , which is the reciprocal of the fraction.
Lesson 11 Practice Problems
Select all statements that show correct reasoning for finding .
- Multiplying by 5 and then by .
- Dividing by 5, and then multiplying by .
- Multiplying by 7, and then multiplying by .
- Multiplying by 5 and then dividing by 7.
Clare said that is . She reasoned: and .
Explain why Clare’s answer and reasoning are incorrect. Find the correct quotient.
Find the value of . Show your reasoning.
Kiran has pounds of flour. When he divides the flour into equal-sized bags, he fills bags. How many pounds fit in each bag?
Write a multiplication equation and a division equation to represent the question and then answer the question. Show your reasoning.Divide by the following unit fractions.
a.
b.
c.
After charging for of an hour, a phone is at of its full power. How long will it take the phone to charge completely?
Decide whether each equation can represent the situation.
Elena and Noah are each filling a bucket with water. Noah’s bucket is full and the water weighs pounds. How much does Elena’s bucket weigh if her bucket is full and her bucket is identical to Noah’s?
- Write multiplication and division equations to represent the question.
- Draw a diagram to show the relationship between the quantities and to answer the question.