Lesson 4Applying Circumference
Let’s use to solve problems.
Learning Targets:
- I can choose an approximation for based on the situation or problem.
- If I know the radius, diameter, or circumference of a circle, I can find the other two.
4.1 What Do We Know? What Can We Estimate?
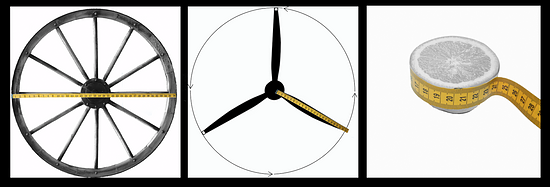
Here are some pictures of circular objects, with measurement tools shown. The measurement tool on each picture reads as follows:
- Wagon wheel: 3 feet
- Plane propeller: 24 inches
- Sliced Orange: 20 centimeters
-
For each picture, which measurement is shown?
-
Based on this information, what measurement(s) could you estimate for each picture?
4.2 Using
In the previous activity, we looked at pictures of circular objects. One measurement for each object is listed in the table.
Your teacher will assign an approximation for for you to use in this activity.
- Complete the table.
object radius diameter circumference wagon wheel 3 ft airplane propeller 24 in orange slice 20 cm -
A bug was sitting on the tip of a wind turbine blade that was 24 inches long when it started to rotate. The bug held on for 5 rotations before flying away. How far did the bug travel before it flew off?
- If you choose to, you can change the settings in the applet and enter your calculation in the box at the bottom to check your work.
- Just for fun, use the slider marked “turn,” and the other one that will appear, to watch the bug’s motion.
4.3 Around the Running Track
The field inside a running track is made up of a rectangle that is 84.39 m long and 73 m wide, together with a half-circle at each end.
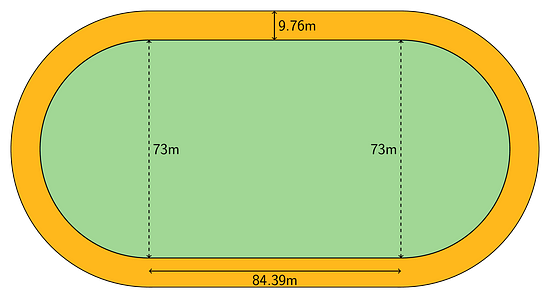
- What is the distance around the inside of the track? Explain or show your reasoning.
- The track is 9.76 m wide all the way around. What is the distance around the outside of the track? Explain or show your reasoning.
Are you ready for more?
This size running track is usually called a 400-meter track. However, if a person ran as close to the “inside” as possible on the track, they would run less than 400 meters in one lap. How far away from the inside border would someone have to run to make one lap equal exactly 400 meters?
4.4 Measuring a Picture Frame
Kiran bent some wire around a rectangle to make a picture frame. The rectangle is 8 inches by 10 inches.

- Find the perimeter of the wire picture frame. Explain or show your reasoning.
- If the wire picture frame were stretched out to make one complete circle, what would its radius be?
Lesson 4 Summary
The circumference of a circle, , is times the diameter, . The diameter is twice the radius, . So if we know any one of these measurements for a particular circle, we can find the others. We can write the relationships between these different measures using equations:
If the diameter of a car tire is 60 cm, that means the radius is 30 cm and the circumference is or about 188 cm.
If the radius of a clock is 5 in, that means the diameter is 10 in, and the circumference is or about 31 in.
If a ring has a circumference of 44 mm, that means the diameter is , which is about 14 mm, and the radius is about 7 mm.
Lesson 4 Practice Problems
Here is a picture of a Ferris wheel. It has a diameter of 80 meters.

“Steiger Ferris Wheel 1102009 1” by Zonk43 via Wikimedia Commons. Public Domain. -
On the picture, draw and label a diameter.
-
How far does a rider travel in one complete rotation around the Ferris wheel?
-
Identify each measurement as the diameter, radius, or circumference of the circular object. Then, estimate the other two measurements for the circle.
-
The length of the minute hand on a clock is 5 in.
-
The distance across a sink drain is 3.8 cm.
-
The tires on a mining truck are 14 ft tall.
-
The fence around a circular pool is 75 ft long.
-
The distance from the tip of a slice of pizza to the crust is 7 in.
-
Breaking a cookie in half creates a straight side 10 cm long.
-
The length of the metal rim around a glass lens is 190 mm.
-
From the center to the edge of a DVD measures 60 mm.
-
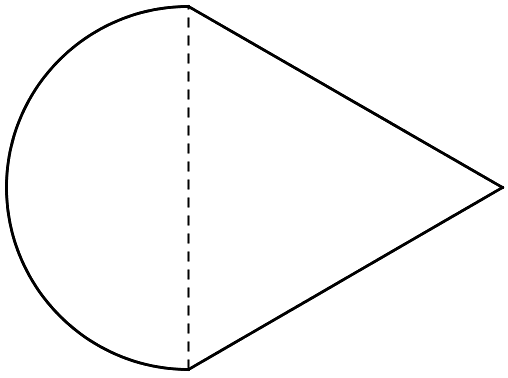
A half circle is joined to an equilateral triangle with side lengths of 12 units. What is the perimeter of the resulting shape?
Circle A has a diameter of 1 foot. Circle B has a circumference of 1 meter. Which circle is bigger? Explain your reasoning. (1 inch = 2.54 centimeters)
The circumference of Tyler's bike tire is 72 inches. What is the diameter of the tire?