Open Up Resources Logo

Lesson 14Decimal Representations of Rational Numbers

Let’s learn more about how rational numbers can be represented. 

Learning Targets:

  • I can write a fraction as a repeating decimal.
  • I understand that every number has a decimal expansion.

14.1 Notice and Wonder: Shaded Bars

What do you notice? What do you wonder?

There are four rectangular bars of equal length, aligned vertically. The first rectangular bar is divided into two equal sized parts and the first part is shaded. The second rectangular bar is divided into 4 equal sized parts and the first part is shaded. The third rectangular bar is divided into 8 equal sized parts and the firts part is shaded. The fourth rectangular bar is divided into 16 equal sized parts and the first bar is shaded.

14.2 Halving the Length

Here is a number line from 0 to 1.

A number line with two tick marks, one on either end of the number line. The first tick mark is labeled "0" and the second tick mark is labeled "1."
  1. Mark the midpoint between 0 and 1. What is the decimal representation of that number?
  2. Mark the midpoint between 0 and the newest point. What is the decimal representation of that number?
  3. Repeat step two. How did you find the value of this number?
  4. Describe how the value of the midpoints you have added to the number line keep changing as you find more. How do the decimal representations change? 

14.3 Recalculating Rational Numbers

  1. Rational numbers are fractions and their opposites. All of these numbers are rational numbers. Show that they are rational by writing them in the form \frac{a}{b} or \text -\frac{a}{b} .

    1. 0.2
    2. \text -\sqrt{4}
    3. 0.333
    4. \sqrt[3]{1000}
    5. -1.000001
    6. \sqrt{\frac19}

  2. All rational numbers have decimal representations, too. Find the decimal representation of each of these rational numbers.

    1. \frac38
    2. \frac75
    3. \frac{999}{1000}
    4. \frac{111}{2}
    5. \sqrt[3]{\frac18}

14.4 Zooming In On \frac{2}{11}

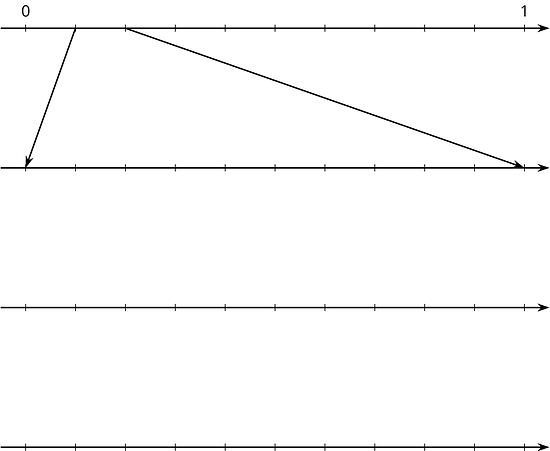
A zooming number line cosisting of 4 number lines, aligned vertically, each with 11 evenly spaced tick marks. On the first number line, the first tick mark is labeled "0" and the 11th tick mark is labeled "1." Two arrows are drawn from the first number line to the second number line. The first arrow is drawn from the second tick mark on the first number line to the first tick mark on the second number line. The second arrow is drawn from the third tick mark on the first number line to the eleventh tick mark on the second number line. There are no numbers inidicated on the second number line. The third and fourth number lines are both unlabeled.

  1. On the topmost number line, label the tick marks. Next, find the first decimal place of  \frac{2}{11} using long division and estimate where \frac{2}{11} should be placed on the top number line.

  2. Label the tick marks of the second number line. Find the next decimal place of \frac{2}{11} by continuing the long division and estimate where \frac{2}{11} should be placed on the second number line. Add arrows from the second to the third number line to zoom in on the location of \frac{2}{11} .

  3. Repeat the earlier step for the remaining number lines.

  4. What do you think the decimal expansion of \frac{2}{11} is?

Are you ready for more?

Let x=\frac{25}{11}=2.272727. . . and y=\frac{58}{33}=1.75757575. . .

For each of the following questions, first decide whether the fraction or decimal representations of the numbers are more helpful to answer the question, and then find the answer.

  • Which of x or y is closer to 2?
  • Find x^2 .

Lesson 14 Summary

We learned earlier that rational numbers are a fraction or the opposite of a fraction. For example, \frac34 and \text-\frac52 are both rational numbers. A complicated-looking numerical expression can also be a rational number as long as the value of the expression is a positive or negative fraction. For example,  \sqrt{64} and \text-\sqrt[3]{\frac18}  are rational numbers because  \sqrt{64} = 8 and \text-\sqrt[3]{\frac18} = \text-\frac12 .

Rational numbers can also be written using decimal notation. Some have finite decimal expansions, like 0.75, -2.5, or -0.5. Other rational numbers have infinite decimal expansions, like 0.7434343 . . . where the 43s repeat forever. To avoid writing the repeating part over and over, we use the notation 0.7\overline{43} for this number. The bar over part of the expansion tells us the part which is to repeat forever.

A decimal expansion of a number helps us plot it accurately on a number line divided into tenths. For example, 0.7\overline{43} should be between 0.7 and 0.8. Each further decimal digit increases the accuracy of our plotting. For example, the number 0.7\overline{43} is between 0.743 and 0.744.

Lesson 14 Practice Problems

  1. Andre and Jada are discussing how to write \frac{17}{20} as a decimal.

    Andre says he can use long division to divide 17 by 20 to get the decimal.

    Jada says she can write an equivalent fraction with a denominator of 100 by multiplying by \frac{5}{5} , then writing the number of hundredths as a decimal.

    1. Do both of these strategies work?

    2. Which strategy do you prefer? Explain your reasoning.

    3. Write \frac{17}{20} as a decimal. Explain or show your reasoning.

  2. Write each fraction as a decimal.

    1. \sqrt{\frac{9}{100}}

    2. \frac{99}{100}

    3. \sqrt{\frac{9}{16}}

    4. \frac{23}{10}

  3. Write each decimal as a fraction.

    1. \sqrt{0.81}

    2. 0.0276

    3. \sqrt{0.04}

    4. 10.01

  4. Find the positive solution to each equation. If the solution is irrational, write the solution using square root or cube root notation.

    1. x^2=90

    2. p^3=90

    3. z^2=1

    4. y^3=1

    5. w^2=36

    6. h^3=64

  5. Here is a right square pyramid.

    A right square pyramid. The side lengths of the square base are labeled 16. The slant height is labeled “L” and is indicated by a dashed line from the top vertex of the pyramid, along the middle of one of the side triangular faces. A right triangle is formed inside the pyramid by the slant height line, “L,” a dashed line from the top vertex of the pyramid, to the middle of the square, labeled 15, and by another dashed line that forms a right angle and connects along the base of the pyramid to the slant height, “L.” The slant height “L” is opposite the right angle.

    1. What is the measurement of the slant height \ell of the triangular face of the pyramid? If you get stuck, use a cross section of the pyramid.

    2. What is the surface area of the pyramid?