Lesson 2Finding Area by Decomposing and Rearranging
Let’s create shapes and find their areas.
Learning Targets:
- I can explain how to find the area of a figure that is composed of other shapes.
- I know how to find the area of a figure by decomposing it and rearranging the parts.
- I know what it means for two figures to have the same area.
2.1 What is Area?
You may recall that the term area tells us something about the number of squares inside a two-dimensional shape.
- Here are four drawings that each show squares inside a shape. Select all drawings whose squares could be used to find the area of the shape. Be prepared to explain your reasoning.
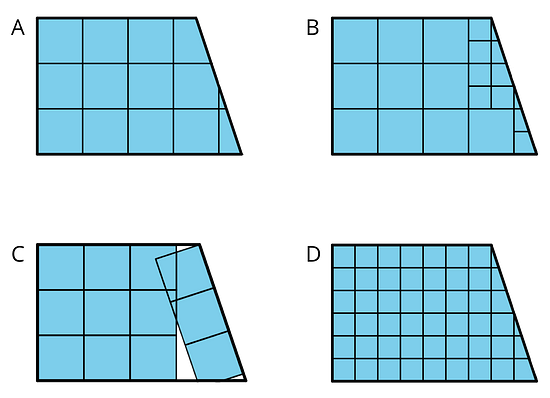
- Write a definition of area that includes all the information that you think is important.
2.2 Composing Shapes
This applet has one square and some small, medium, and large right triangles. The area of the square is 1 square unit.
Click on a shape and drag to move it. Grab the point at the vertex and drag to turn it.
-
Notice that you can put together two small triangles to make a square. What is the area of the square composed of two small triangles? Be prepared to explain your reasoning.
-
Use your shapes to create a new shape with an area of 1 square unit that is not a square. Draw your shape on paper and label it with its area.
-
Use your shapes to create a new shape with an area of 2 square units. Draw your shape and label it with its area.
-
Use your shapes to create a different shape with an area of 2 square units. Draw your shape and label it with its area.
-
Use your shapes to create a new shape with an area of 4 square units. Draw your shape and label it with its area.
Are you ready for more?
Find a way to use all of your pieces to compose a single large square. What is the area of this large square?
2.3 Tangram Triangles
Recall that the area of the square you saw earlier is 1 square unit. Complete each statement and explain your reasoning.
- The area of the small triangle is ____________ square units. I know this because . . .
- The area of the medium triangle is ____________ square units. I know this because . . .
- The area of the large triangle is ____________ square units. I know this because . . .
Lesson 2 Summary
Here are two important principles for finding area:
-
If two figures can be placed one on top of the other so that they match up exactly, then they have the same area.
-
We can decompose a figure (break a figure into pieces) and rearrange the pieces (move the pieces around) to find its area.
Here are illustrations of the two principles.
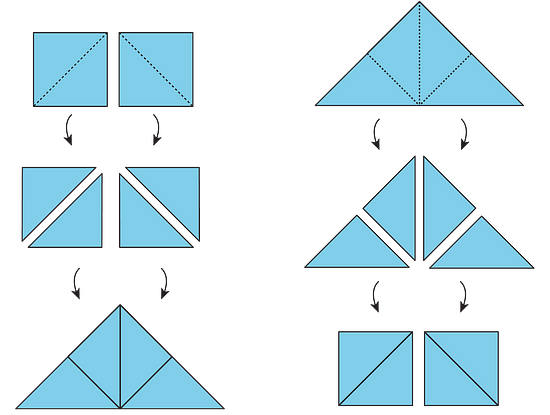
- Each square on the left can be decomposed into 2 triangles. These triangles can be rearranged into a large triangle. So the large triangle has the same area as the 2 squares.
-
Similarly, the large triangle on the right can be decomposed into 4 equal triangles. The triangles can be rearranged to form 2 squares. If each square has an area of 1 square unit, then the area of the large triangle is 2 square units. We also can say that each small triangle has an area of square unit.
Glossary Terms
Area is the number of square units that covers a two-dimensional region, without any gaps or overlaps.
For example, the area of region A is 8 square units. The area of the shaded region of B is square unit.

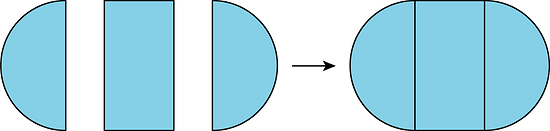
Compose means “put together.” We use the word compose to describe putting more than one figure together to make a new shape.
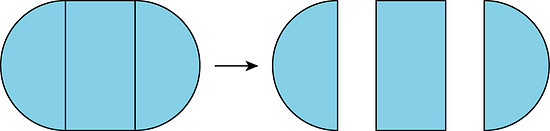
Decompose means “take apart.” We use the word decompose to describe taking a figure apart to make more than one new shape.
Lesson 2 Practice Problems
The diagonal of a rectangle is shown.

-
Decompose the rectangle along the diagonal, and recompose the two pieces to make a different shape.
-
How does the area of this new shape compare to the area of the original rectangle? Explain how you know.
-
The area of the square is 1 square unit. Two small triangles can be put together to make a square or to make a medium triangle.
Which figure also has an area of square units? Select all that apply.

Priya decomposed a square into 16 smaller, equal-size squares and then cut out 4 of the small squares and attached them around the outside of original square to make a new figure.
How does the area of her new figure compare with that of the original square?
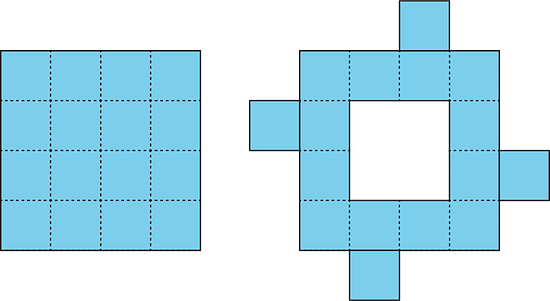
- The area of the new figure is greater.
- The two figures have the same area.
- The area of the original square is greater.
- We don’t know because neither the side length nor the area of the original square is known.
The area of a rectangular playground is 78 square meters. If the length of the playground is 13 meters, what is its width?
A student said, “We can’t find the area of the shaded region because the shape has many different measurements, instead of just a length and a width that we could multiply.”
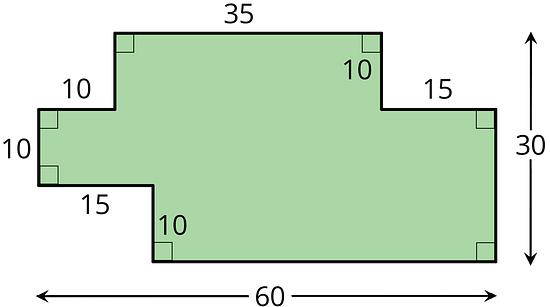
Explain why the student’s statement about area is incorrect.