Lesson 4Parallelograms
Let’s investigate the features and area of parallelograms.
Learning Targets:
- I can use reasoning strategies and what I know about the area of a rectangle to find the area of a parallelogram.
- I know how to describe the features of a parallelogram using mathematical vocabulary.
4.1 Features of a Parallelogram
Figures A, B, and C are parallelograms. Figures D, E, and F are not parallelograms.
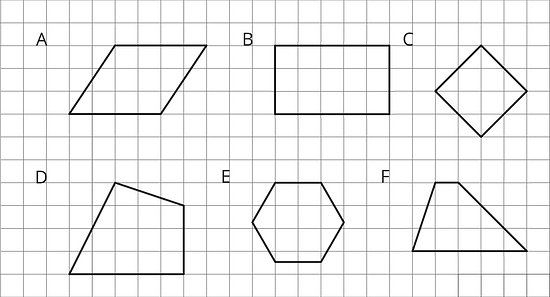
Study the examples and non-examples. What do you notice about:
- the number of sides that a parallelogram has?
- opposite sides of a parallelogram?
- opposite angles of a parallelogram?
4.2 Area of a Parallelogram
- Find the area of the parallelogram and explain your reasoning.
- Change the parallelogram by dragging the green points at its vertices. Find its area and explain your reasoning.
- If you used the polygons on the side, how were they helpful? If you did not, could you use one or more of the polygons to show another way to find the area of the parallelogram?
4.3 Lots of Parallelograms
Find the area of the following parallelograms. Show your reasoning.
Lesson 4 Summary
A parallelogram is a quadrilateral (it has four sides). The opposite sides of a parallelogram are parallel. It is also true that:
- The opposite sides of a parallelogram have equal length.
- The opposite angles of a parallelogram have equal measure.

There are several strategies for finding the area of a parallelogram.
- We can decompose and rearrange a parallelogram to form a rectangle. Here are three ways:

- We can enclose the parallelogram and then subtract the area of the two triangles in the corner.

Both of these ways will work for any parallelogram.
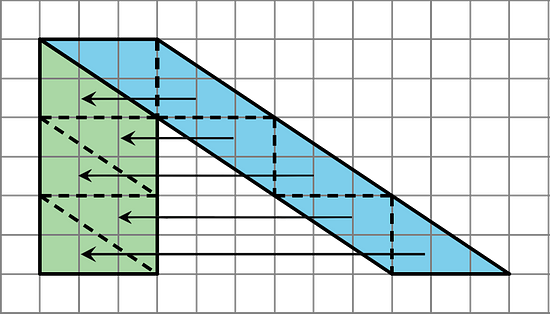
For some parallelograms, however, the process of decomposing and rearranging requires a lot more steps than if we enclose the parallelogram with a rectangle and subtract the combined area of the two triangles in the corners. Here is an example.
Glossary Terms
A parallelogram is a type of quadrilateral that has two pairs of parallel sides.
Here are two examples of parallelograms.

Lesson 4 Practice Problems
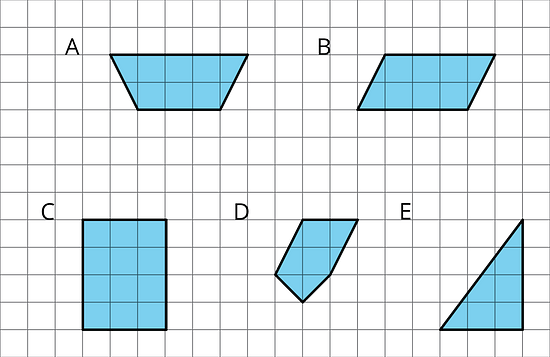
Select all of the parallelograms. For each figure that is not selected, explain how you know it is not a parallelogram.
a. Decompose and rearrange this parallelogram to make a rectangle.
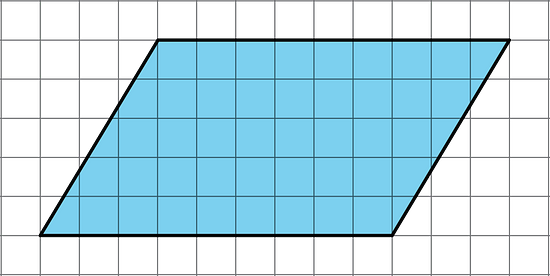
b. What is the area of the parallelogram? Explain your reasoning.
Find the area of the parallelogram.

Explain why this quadrilateral is not a parallelogram.
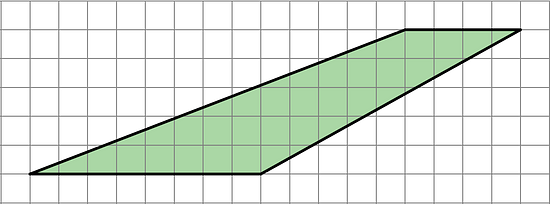
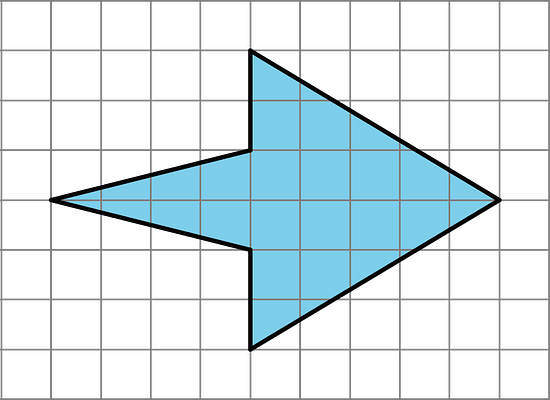
Find the area of each shape. Show your reasoning.

Find the areas of the rectangles with the following side lengths.
-
5 in and in
-
5 in and in
-
in and in
-
in and in
-