Lesson 15Part-Part-Whole Ratios
Let’s look at situations where you can add the quantities in a ratio together.
Learning Targets:
- I can create tape diagrams to help me reason about problems involving a ratio and a total amount.
- I can solve problems when I know a ratio and a total amount.
15.1 True or False: Multiplying by a Unit Fraction
True or false?
15.2 Cubes of Paint
A recipe for maroon paint says, “Mix 5 ml of red paint with 3 ml of blue paint.”
- Use snap cubes to represent the amounts of red and blue paint in the recipe. Then, draw a sketch of your snap-cube representation of the maroon paint.
- What amount does each cube represent?
- How many milliliters of maroon paint will there be?
-
-
Suppose each cube represents 2 ml. How much of each color paint is there?
Red: _______ ml
Blue: _______ ml
Maroon: _______ ml
-
Suppose each cube represents 5 ml. How much of each color paint is there?
Red: _______ ml
Blue: _______ ml
Maroon: _______ ml
-
-
-
Suppose you need 80 ml of maroon paint. How much red and blue paint would you mix? Be prepared to explain your reasoning.
Red: _______ ml
Blue: _______ ml
Maroon: 80 ml
- If the original recipe is for one batch of maroon paint, how many batches are in 80 ml of maroon paint?
-
15.3 Sneakers, Chicken, and Fruit Juice
Solve each of the following problems and show your thinking. If you get stuck, consider drawing a tape diagram to represent the situation.
- The ratio of students wearing sneakers to those wearing boots is 5 to 6. If there are 33 students in the class, and all of them are wearing either sneakers or boots, how many of them are wearing sneakers?
- A recipe for chicken marinade says, “Mix 3 parts oil with 2 parts soy sauce and 1 part orange juice.” If you need 42 cups of marinade in all, how much of each ingredient should you use?
- Elena makes fruit punch by mixing 4 parts cranberry juice to 3 parts apple juice to 2 parts grape juice. If one batch of fruit punch includes 30 cups of apple juice, how large is this batch of fruit punch?
Are you ready for more?
15.4 Invent Your Own Ratio Problem
- Invent another ratio problem that can be solved with a tape diagram and solve it. If you get stuck, consider looking back at the problems you solved in the earlier activity.
-
Create a visual display that includes:
- The new problem that you wrote, without the solution.
- Enough work space for someone to show a solution.
-
Trade your display with another group, and solve each other’s problem. Include a tape diagram as part of your solution. Be prepared to share the solution with the class.
-
When the solution to the problem you invented is being shared by another group, check their answer for accuracy.
Lesson 15 Summary
A tape diagram is another way to represent a ratio. All the parts of the diagram that are the same size have the same value.
For example, this tape diagram represents the ratio of ducks to swans in a pond, which is .
The first tape represents the number of ducks. It has 4 parts.
The second tape represents the number of swans. It has 5 parts.
There are 9 parts in all, because .
Suppose we know there are 18 of these birds in the pond, and we want to know how many are ducks.
The 9 equal parts on the diagram need to represent 18 birds in all. This means that each part of the tape diagram represents 2 birds, because .
There are 4 parts of the tape representing ducks, and , so there are 8 ducks in the pond.
Glossary Terms
A tape diagram is a group of rectangles put together to represent a relationship between quantities.
For example, this tape diagram shows a ratio of 30 gallons of yellow paint to 50 gallons of blue paint.
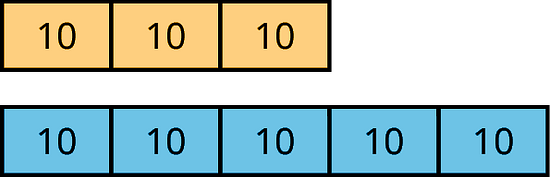
If each rectangle were labeled 5, instead of 10, then the same picture could represent the equivalent ratio of 15 gallons of yellow paint to 25 gallons of blue paint.
Lesson 15 Practice Problems
Here is a tape diagram representing the ratio of red paint to yellow paint in a mixture of orange paint.
- What is the ratio of yellow paint to red paint?
- How many total cups of orange paint will this mixture yield?
At the kennel, the ratio of cats to dogs is . There are 27 animals in all. Here is a tape diagram representing this ratio.
- What is the value of each small rectangle?
- How many dogs are at the kennel?
- How many cats are at the kennel?
- Last month, there were 4 sunny days for every rainy day. If there were 30 days in the month, how many days were rainy? Explain your reasoning. If you get stuck, consider using a tape diagram.
Noah entered a 100-mile bike race. He knows he can ride 32 miles in 160 minutes. At this rate, how long will it take him to finish the race? Use each table to find the answer. Next, explain which table you think works better in finding the answer.
Table A:
distance (miles) elapsed time (minutes) 32 160 1 100 Table B:
distance (miles) elapsed time (minutes) 32 160 96 4 100 A cashier worked an 8-hour day, and earned $58.00. The double number line shows the amount she earned for working different numbers of hours. For each question, explain your reasoning.
- How much does the cashier earn per hour?
- How much does the cashier earn if she works 3 hours?
A grocery store sells bags of oranges in two different sizes.
- The 3-pound bags of oranges cost $4.
- The 8-pound bags of oranges for $9.
Which oranges cost less per pound? Explain or show your reasoning.