Lesson 3Recipes
Let’s explore how ratios affect the way a recipe tastes.
Learning Targets:
- I can explain the meaning of equivalent ratios using a recipe as an example.
- I can use a diagram to represent a recipe, a double batch, and a triple batch of a recipe.
- I know what it means to double or triple a recipe.
3.1 Flower Pattern
This flower is made up of yellow hexagons, red trapezoids, and green triangles.
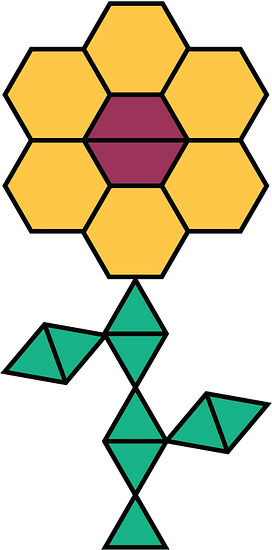
- Write sentences to describe the ratios of the shapes that make up this pattern.
- How many of each shape would be in two copies of this flower pattern?
3.2 Powdered Drink Mix
Here are diagrams representing three mixtures of powdered drink mix and water:
-
How would the taste of Mixture A compare to the taste of Mixture B?
-
Use the diagrams to complete each statement:
-
Mixture B uses ______ cups of water and ______ teaspoons of drink mix. The ratio of cups of water to teaspoons of drink mix in Mixture B is ________.
-
Mixture C uses ______ cups of water and ______ teaspoons of drink mix. The ratio of cups of water to teaspoons of drink mix in Mixture C is ________.
-
- How would the taste of Mixture B compare to the taste of Mixture C?
Are you ready for more?
Sports drinks use sodium (better known as salt) to help people replenish electrolytes. Here are the nutrition labels of two sports drinks.
- Which of these drinks is saltier? Explain how you know.
- If you wanted to make sure a sports drink was less salty than both of the ones given, what ratio of sodium to water would you use?
3.3 Batches of Cookies
A recipe for one batch of cookies calls for 5 cups of flour and 2 teaspoons of vanilla.
- Draw a diagram that shows the amount of flour and vanilla needed for two batches of cookies.
- How many batches can you make with 15 cups of flour and 6 teaspoons of vanilla? Indicate the additional batches by adding more ingredients to your diagram.
- How much flour and vanilla would you need for 5 batches of cookies?
-
Whether the ratio of cups of flour to teaspoons of vanilla is , , or , the recipes would make cookies that taste the same. We call these equivalent ratios.
-
Find another ratio of cups of flour to teaspoons of vanilla that is equivalent to these ratios.
-
How many batches can you make using this new ratio of ingredients?
-
Lesson 3 Summary
A recipe for fizzy juice says, “Mix 5 cups of cranberry juice with 2 cups of soda water.”
To double this recipe, we would use 10 cups of cranberry juice with 4 cups of soda water. To triple this recipe, we would use 15 cups of cranberry juice with 6 cups of soda water.
This diagram shows a single batch of the recipe, a double batch, and a triple batch:

We say that the ratios , , and are equivalent. Even though the amounts of each ingredient within a single, double, or triple batch are not the same, they would make fizzy juice that tastes the same.
Lesson 3 Practice Problems
A recipe for 1 batch of spice mix says, “Combine 3 teaspoons of mustard seeds, 5 teaspoons of chili powder, and 1 teaspoon of salt.” How many batches are represented by the diagram? Explain or show your reasoning.
Priya makes chocolate milk by mixing 2 cups of milk and 5 tablespoons of cocoa powder. Draw a diagram that clearly represents two batches of her chocolate milk.
In a recipe for fizzy grape juice, the ratio of cups of sparkling water to cups of grape juice concentrate is 3 to 1.
- Find two more ratios of cups of sparkling water to cups of juice concentrate that would make a mixture that tastes the same as this recipe.
- Describe another mixture of sparkling water and grape juice that would taste different than this recipe.
Write the missing number under each tick mark on the number line.
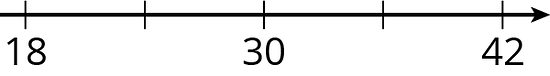
At the kennel, there are 6 dogs for every 5 cats.
- The ratio of dogs to cats is ______ to ______.
- The ratio of cats to dogs is ______ to ______.
- For every ______ dogs there are ______ cats.
- The ratio of cats to dogs is ______ : ______.
Elena has 80 unit cubes. What is the volume of the largest cube she can build with them?
Fill in the blanks to make each equation true.
(As long as does not equal 0.)