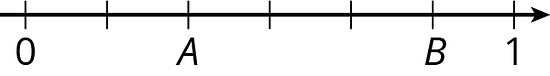Open Up Resources Logo

Lesson 5Defining Equivalent Ratios

Let’s investigate equivalent ratios some more.

Learning Targets:

  • If I have a ratio, I can create a new ratio that is equivalent to it.
  • If I have two ratios, I can decide whether they are equivalent to each other.

5.1 Dots and Half Dots

Dot Pattern 1:

(Tactile is recommended for this image) An image of dots arranged in groups. There are 6 groups of 9 dots arranged in a 3 by 3 square pattern.

Dot Pattern 2:

(A tactile is recommended for this image.) An image of half-dots arranged in columns and rows. There are 6 columns of 7 half-dots.

5.2 Tuna Casserole

Here is a recipe for tuna casserole.

Ingredients

  • 3 cups cooked elbow-shaped pasta
  • 6 ounce can tuna, drained
  • 10 ounce can cream of chicken soup
  • 1 cup shredded cheddar cheese
  • 1 \frac12 cups French fried onions
an image of a Sausage Egg Casserole
“Sausage Egg Casserole” by RBerteig via Flickr. CC BY 2.0.

Instructions

Combine the pasta, tuna, soup, and half of the cheese. Transfer into a 9-inch-by-18-inch baking dish. Put the remaining cheese on top. Bake 30 minutes at 350 degrees. During the last 5 minutes, add the French fried onions. Let sit for 10 minutes before serving.

  1. What is the ratio of the ounces of soup to the cups of shredded cheese to the cups of pasta in one batch of casserole?
  2. How much of each of these 3 ingredients would be needed to make:
    1. twice the amount of casserole?
    2. half the amount of casserole?
    3. five times the amount of casserole?
    4. one-fifth the amount of casserole?
  3. What is the ratio of cups of pasta to ounces of tuna in one batch of casserole?

  4. How many batches of casserole would you make if you used the following amounts of ingredients?

    1. 9 cups of pasta and 18 ounces of tuna?
    2. 36 ounces of tuna and 18 cups of pasta?
    3. 1 cup of pasta and 2 ounces of tuna?

Are you ready for more?

The recipe says to use a 9 inch by 18 inch baking dish. Determine the length and width of a baking dish with the same height that could hold:

  1. Twice the amount of casserole
  2. Half the amount of casserole
  1. Five times the amount of casserole
  2. One-fifth the amount of casserole

5.3 What Are Equivalent Ratios?

The ratios  5:3 and 10:6 are equivalent ratios.

  1. Is the ratio 15:12 equivalent to these? Explain your reasoning.
  2. Is the ratio 30:18 equivalent to these? Explain your reasoning.
  3. Give two more examples of ratios that are equivalent to 5:3 .
  4. How do you know when ratios are equivalent and when they are not equivalent?

  5. Write a definition of equivalent ratios.

    Pause here so your teacher can review your work and assign you a ratio to use for your visual display.

  6. Create a visual display that includes:

    • the title “Equivalent Ratios”
    • your best definition of equivalent ratios
    • the ratio your teacher assigned to you
    • at least two examples of ratios that are equivalent to your assigned ratio
    • an explanation of how you know these examples are equivalent
    • at least one example of a ratio that is not equivalent to your assigned ratio
    • an explanation of how you know this example is not equivalent
    Be prepared to share your display with the class.

Lesson 5 Summary

All ratios that are equivalent to a:b can be made by multiplying both a and b by the same number.

For example, the ratio 18:12 is equivalent to 9:6 because both 9 and 6 are multiplied by the same number: 2.

A diagram for a ratio. At the top, the expression 9:6 is indicated. Directly below it, the expression 18:12 is indicated. Two arrows are drawn, one starting at 9 and pointing to 18 and the other starting at 6 and pointing to 12. On the left of the first arrow, multiplied by 2 is labeled and to the right of the second arrow, multiplied by 2 is labeled.

3:2 is also equivalent to 9:6 , because both 9 and 6 are multiplied by the same number: \frac13 .

“”

Is 18:15 equivalent to 9:6 ?

No, because 18 is 9 \boldcdot 2 , but 15 is not 6 \boldcdot 2 .

“”

Glossary Terms

equivalent ratios

Two ratios are equivalent if you can multiply each of the numbers in the first ratio by the same factor to get the numbers in the second ratio. For example, 8:6 is equivalent to 4:3 , because 8\boldcdot\frac12 = 4 and 6\boldcdot\frac12 = 3 .

A recipe for lemonade says to use 8 cups of water and 6 lemons. If we use 4 cups of water and 3 lemons, it will make half as much lemonade. Both recipes taste the same, because 8:6 and 4:3 are equivalent ratios.

cups of water number of lemons
8 6
4 3

Lesson 5 Practice Problems

  1. Each of these is a pair of equivalent ratios. For each pair, explain why they are equivalent ratios or draw a diagram that shows why they are equivalent ratios.

    1. 4:5 and 8:10
    2. 18:3 and  6:1
    1. 2:7 and 10,\!000:35,\!000

  2. Explain why 6:4 and 18:8 are not equivalent ratios.

  3. Are the ratios 3:6 and 6:3 equivalent? Why or why not?

  4. This diagram represents 3 batches of light yellow paint. Draw a diagram that represents 1 batch of the same shade of light yellow paint.

    A discrete diagram for two quantities labeled "white paint, in cups" and "yellow paint, in cups". The data are as follows: white paint, 9 squares. yellow paint, 15 squares.

  5. In the fruit bowl there are 6 bananas, 4 apples, and 3 oranges.

    1. For every 4 __________________, there are 3 __________________.
    2. The ratio of __________________ to __________________ is 6:3 .
    3. The ratio of __________________ to __________________ is 4 to 6.
    4. For every 1 orange, there are ______ bananas.

  6. Write fractions for points A and B on the number line.

    A number line with points A and B