Lesson 1The Burj Khalifa
Let’s investigate the Burj Khalifa building.
Learning Targets:
- I can see that thinking about “how much for 1” is useful for solving different types of problems.
1.1 Estimating Height
Use the picture to estimate the height of Hyperion, the tallest known tree.

1.2 Window Washing

A window-washing crew can finish 15 windows in 18 minutes.
If this crew was assigned to wash all the windows on the outside of the Burj Khalifa, how long will the crew be washing at this rate?
1.3 Climbing the Burj Khalifa
In 2011, a professional climber scaled the outside of the Burj Khalifa, making it all the way to 828 meters (the highest point on which a person can stand) in 6 hours.
Assuming they climbed at the same rate the whole way:
- How far did they climb in the first 2 hours?
- How far did they climb in 5 hours?
- How far did they climb in the final 15 minutes?
Are you ready for more?
Have you ever seen videos of astronauts on the moon jumping really high?
An object on the moon weighs less than it does on Earth because the moon has much less mass than Earth.
-
A woman who weighs 160 pounds on Earth weighs 30 pounds on the moon. If a boy weighs 60 pounds on Earth, how much does he weigh on the moon?
- Every 10 pounds on Earth are the equivalent to 4 pounds on Mars. If the same woman travels to Mars, how much would she weigh there?
Lesson 1 Summary
There are many real-world situations in which something keeps happening at the same rate. For example:
- a bus stop that is serviced by 4 buses per hour
- a washing machine that takes 45 minutes per load of laundry
- a school cafeteria that serves 15 students per minute
In situations like these, we can use equivalent ratios to predict how long it will take for something to happen some number of times, or how many times it will happen in a particular length of time.
-
How long will it take the school cafeteria to serve 600 students?
The table shows that it will take the cafeteria 40 minutes to serve 600 students.
number of students time in minutes 15 1 60 4 600 40 -
How many students can the cafeteria serve in 1 hour?
The double number line shows that the cafeteria can serve 900 students in 1 hour.
Lesson 1 Practice Problems
An elevator travels 310 feet in 10 seconds. At that speed, how far can this elevator travel in 12 seconds? Explain your reasoning.
Han earns $33.00 for babysitting 4 hours. At this rate, how much will he earn if he babysits for 7 hours? Explain your reasoning.
The cost of 5 cans of dog food is $4.35. At this price, how much do 11 cans of dog food cost? Explain your reasoning.
A restaurant has 26 tables in its dining room. It takes the waitstaff 10 minutes to clear and set 4 tables. At this rate, how long will it take the waitstaff to clear and set all the tables in the dining room? Explain or show your reasoning.
A sandwich shop serves 4 ounces of meat and 3 ounces of cheese on each sandwich. After making sandwiches for an hour, the shop owner has used 91 combined ounces of meat and cheese.
-
How many combined ounces of meat and cheese are used on each sandwich?
- How many sandwiches were made in the hour?
- How many ounces of meat were used?
- How many ounces of cheese were used?
-
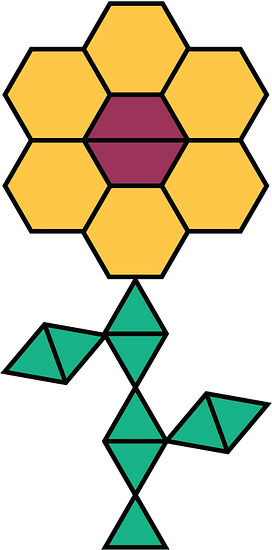
Here is a flower made up of yellow hexagons, red trapezoids, and green triangles.
- How many copies of this flower pattern could you build if you had 30 yellow hexagons, 50 red trapezoids, and 60 green triangles?
- Of which shape would you have the most left over?
Match each quantity in the first list with an appropriate unit of measurement from the second list.
- the perimeter of a baseball field
- the area of a bed sheet
- the volume of a refrigerator
- the surface area of a tissue box
- the length of a spaghetti noodle
- the volume of a large lake
- the surface area of the moon
- centimeters (cm)
- cubic feet (cu ft)
- cubic kilometers (cu km)
- meters (m)
- square feet (sq ft)
- square inches (sq in)
- square kilometers (sq km)