Lesson 13Benchmark Percentages
Let’s contrast percentages and fractions.
Learning Targets:
- When I read or hear that something is 10%, 25%, 50%, or 75% of an amount, I know what fraction of that amount they are referring to.
13.1 What Percentage Is Shaded?
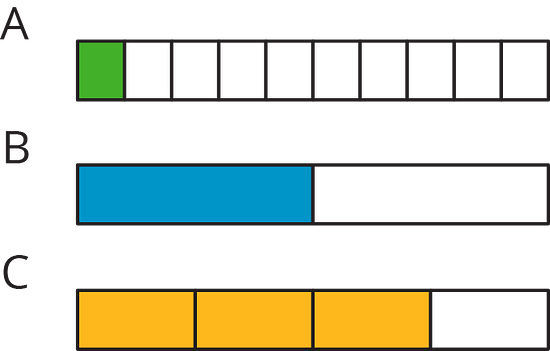
What percentage of each diagram is shaded?
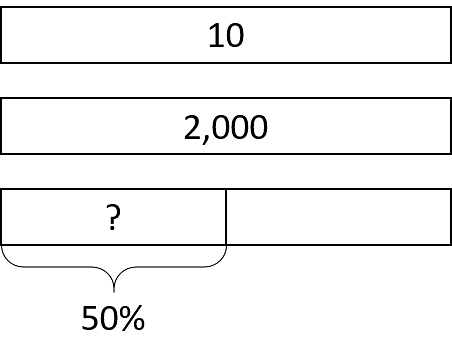
13.2 Liters, Meters, and Hours
-
- How much is 50% of 10 liters of milk?
- How far is 50% of a 2,000-kilometer trip?
- How long is 50% of a 24-hour day?
- How can you find 50% of any number?
-
- How far is 10% of a 2,000-kilometer trip?
- How much is 10% of 10 liters of milk?
- How long is 10% of a 24-hour day?
- How can you find 10% of any number?
-
- How long is 75% of a 24-hour day?
- How far is 75% of a 2,000-kilometer trip?
- How much is 75% of 10 liters of milk?
- How can you find 75% of any number?
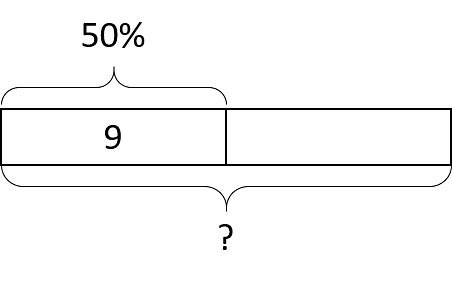
13.3 Nine is . . .
Explain how you can calculate each value mentally.
- 9 is 50% of what number?
- 9 is 25% of what number?
- 9 is 10% of what number?
- 9 is 75% of what number?
- 9 is 150% of what number?
13.4 Matching the Percentage
Match the percentage that describes the relationship between each pair of numbers. One percentage will be left over. Be prepared to explain your reasoning.
-
7 is what percentage of 14?
-
5 is what percentage of 20?
-
3 is what percentage of 30?
-
6 is what percentage of 8?
-
20 is what percentage of 5?
- 4%
- 10%
- 25%
- 50%
- 75%
- 400%
Are you ready for more?
- What percentage of the world’s current population is under the age of 14?
- How many people is that?
- How many people are 14 or older?
Lesson 13 Summary
Certain percentages are easy to think about in terms of fractions.
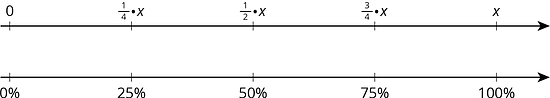
- 25% of a number is always of that number.
For example, 25% of 40 liters is or 10 liters. - 50% of a number is always of that number.
For example, 50% of 82 kilometers or 41 kilometers. - 75% of a number is always of that number.
For example, 75% of 1 pound is pound. - 10% of a number is always of that number.
For example, 10% of 95 meters is 9.5 meters. - We can also find multiples of 10% using tenths.
For example, 70% of a number is always of that number, so 70% of 30 days is or 21 days.

Lesson 13 Practice Problems
-
How can you find 50% of a number quickly in your head?
-
Andre lives 1.6 km from school. What is 50% of 1.6 km?
-
Diego lives mile from school. What is 50% of mile?
-
There is a 10% off sale on laptop computers. If someone saves $35 on a laptop, what was its original cost? If you get stuck, consider using the table.
savings (dollars) percentage 35 10 ? 100 Explain how to calculate these mentally.
- 15 is what percentage of 30?
- 3 is what percentage of 12?
- 6 is what percentage of 10?
- Noah says that to find 20% of a number he divides the number by 5. For example, 20% of 60 is 12, because . Does Noah’s method always work? Explain why or why not.
Diego has 75% of $10. Noah has 25% of $30. Diego thinks he has more money than Noah, but Noah thinks they have an equal amount of money. Who is right? Explain your reasoning.
Lin and Andre start walking toward each other at the same time from opposite ends of 22-mile walking trail. Lin walks at a speed of 2.5 miles per hour. Andre walks at a speed of 3 miles per hour.
Here is a table showing the distances traveled and how far apart Lin and Andre were over time. Use the table to find how much time passes before they meet.
elapsed time (hour) Lin’s distance (miles) Andre’s distance (miles) distance apart (miles) 0 0 0 22 1 2.5 3 16.5 0