Lesson 5How Many Groups? (Part 2)
Let’s use blocks and diagrams to understand more about division with fractions.
Learning Targets:
- I can find how many groups there are when the number of groups and the amount in each group are not whole numbers.
5.1 Reasoning with Fraction Strips
Write a fraction or whole number as an answer for each question. If you get stuck, use the fraction strips. Be prepared to share your strategy.
- How many s are in 2?
- How many s are in 3?
- How many s are in ?
5.2 More Reasoning with Pattern Blocks
Use the pattern blocks in the applet to answer the questions. (If you need help aligning the pieces, you can turn on the grid.)
- If the trapezoid represents 1 whole, what do each of the following shapes represent? Be prepared to show or explain your reasoning.
-
1 triangle
-
1 rhombus
-
1 hexagon
-
-
Use pattern blocks to represent each multiplication equation. Use the trapezoid to represent 1 whole.
-
-
Diego and Jada were asked “How many rhombuses are in a trapezoid?”
- Diego says, “. If I put 1 rhombus on a trapezoid, the leftover shape is a triangle, which is of the trapezoid.”
- Jada says, “I think it’s . Since we want to find out ‘how many rhombuses,’ we should compare the leftover triangle to a rhombus. A triangle is of a rhombus.”
-
Select all equations that can be used to answer the question: “How many rhombuses are in a trapezoid?”
-
5.3 Drawing Diagrams to Show Equal-sized Groups
For each situation, draw a diagram for the relationship of the quantities to help you answer the question. Then write a multiplication equation or a division equation for the relationship. Be prepared to share your reasoning.
- The distance around a park is miles. Noah rode his bicycle around the park for a total of 3 miles. How many times around the park did he ride?
- You need yard of ribbon for one gift box. You have 3 yards of ribbon. How many gift boxes do you have ribbon for?
- The water hose fills a bucket at gallon per minute. How many minutes does it take to fill a 2-gallon bucket?
Are you ready for more?
Lesson 5 Summary
Suppose one batch of cookies requires cup flour. How many batches can be made with 4 cups of flour?
We can think of the question as being: “How many s are in 4?” and represent it using multiplication and division equations.
Let’s use pattern blocks to visualize the situation and say that a hexagon is 1 whole.

Since 3 rhombuses make a hexagon, 1 rhombus represents and 2 rhombuses represent . We can see that 6 pairs of rhombuses make 4 hexagons, so there are 6 groups of in 4.
Other kinds of diagrams can also help us reason about equal-sized groups involving fractions. This example shows how we might reason about the same question from above: “How many -cups are in 4 cups?”
We can see each “cup” partitioned into thirds, and that there are 6 groups of -cup in 4 cups. In both diagrams, we see that the unknown value (or the “?” in the equations) is 6. So we can now write:
Lesson 5 Practice Problems
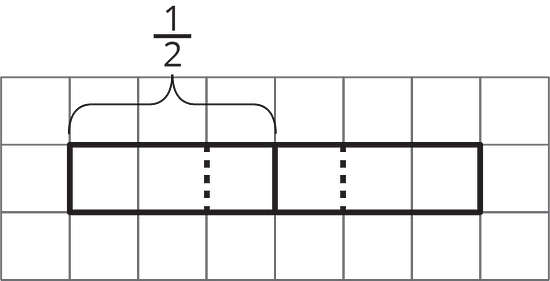
Use the tape diagram to represent and find the value of .
Mark up and label the diagram as needed.
What is the value of ? Use pattern blocks to represent and find this value. The yellow hexagon represents 1 whole. Explain or show your reasoning.

Use a standard inch ruler to answer each question. Then, write a multiplication equation and a division equation that answer the question.
-
How many s are in 7?
-
How many s are in 6?
-
How many s are in ?
-
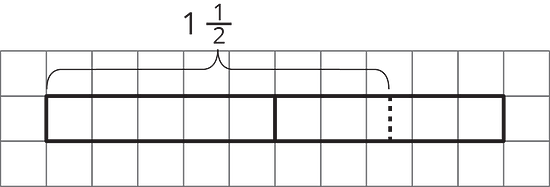
Use the tape diagram to represent and answer the question: How many s are in ?
Mark up and label the diagram as needed.
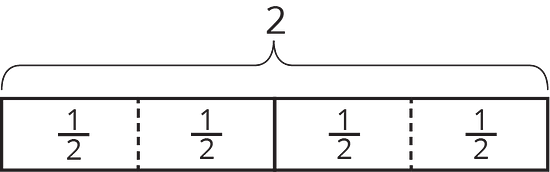
Write a multiplication equation and a division equation to represent each question, statement, or diagram.
- There are 12 fourths in 3.
-
- How many s are in 6?
-
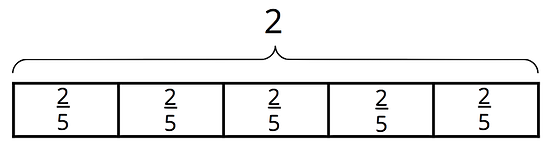
At a farmer’s market, two vendors sell fresh milk. One vendor sells 2 liters for $3.80, and another vendor sells 1.5 liters for $2.70. Which is the better deal? Explain your reasoning.
A recipe uses 5 cups of flour for every 2 cups of sugar.
- How much sugar is used for 1 cup of flour?
- How much flour is used for 1 cup of sugar?
- How much flour is used with 7 cups of sugar?
- How much sugar is used with 6 cups of flour?