Lesson 13Dividing Decimals by Decimals
Let’s divide decimals by decimals.
Learning Targets:
- I can explain how multiplying dividend and divisor by the same power of 10 can help me find a quotient of two decimals.
- I can find the quotient of two decimals.
13.1 Same Values
- Use long division to find the value of .
-
Which of the following quotients has the same value as ? Be prepared to explain how you know.
13.2 Placing Decimal Points in Quotients
- Think of one or more ways to find . Show your reasoning.
- Find . Show your reasoning. If you get stuck, think about what equivalent division expression you could write to help you divide.
-
Diego said, “To divide decimals, we can start by moving the decimal point in both the dividend and divisor by the same number of places and in the same direction. Then we find the quotient of the resulting numbers.”
Do you agree with Diego’s statement? Use the division expression to support your answer.
Are you ready for more?
Can we create an equivalent division expression by multiplying both the dividend and divisor by a number that is not a multiple of 10 (for example: 4, 20, or )? Would doing so produce the same quotient? Explain or show your reasoning.
13.3 Two Ways to Calculate Quotients of Decimals
-
Here are two calculations of . Work with your partner to answer the following questions.
- How are the two calculations alike? How are they different?
- Look at Calculation A. Explain how you can tell that the 36 means “36 tenths” and the 18 means “18 hundredths.”
- Look at Calculation B. What do the 3600 and 1800 mean?
- We can think of as saying “there are 9 groups of 5.42 in 48.78.” We can think of as saying “there are 900 groups of 5.42 in 4878.” How might we show that both statements are true?
-
- Explain why has the same value as .
- Write a division expression that has the same value as but is easier to use to find the value. Then, find the value using long division.
13.4 Practicing Division with Decimals
Find each quotient using a method of your choice. Then discuss your calculations with your group and agree on the correct answers. If someone in your group makes an error, stop and help that person revise their work. If your group is unsure about an answer, consult your teacher.
-
Mai is making friendship bracelets. Each bracelet is made from 24.3 cm of string. If she has 170.1 cm of string, how many bracelets can she make? Explain or show your reasoning.
Lesson 13 Summary
One way to find a quotient of two decimals is to multiply each decimal by a power of 10 so that both products are whole numbers.
If we multiply both decimals by the same power of 10, this does not change the value of the quotient. For example, the quotient can be found by multiplying the two decimals by 10 (or by 100) and instead finding or .
To calculate , which is equivalent to , we could use base-ten diagrams, partial quotients, or long division. Here is the calculation with long division:
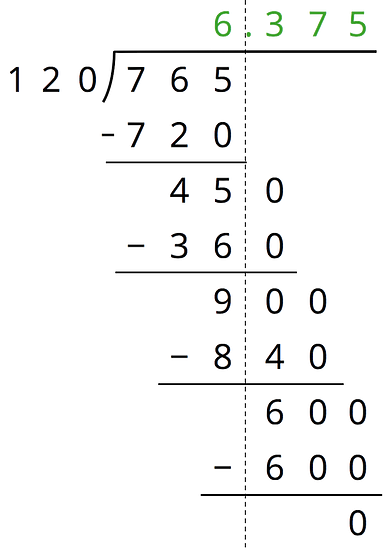
Lesson 13 Practice Problems
A student said, “To find the value of , I can divide 1,092 by 60.”
- Do you agree with this statement? Explain your reasoning.
- Calculate the quotient of using any method of your choice.
Here is how Han found :
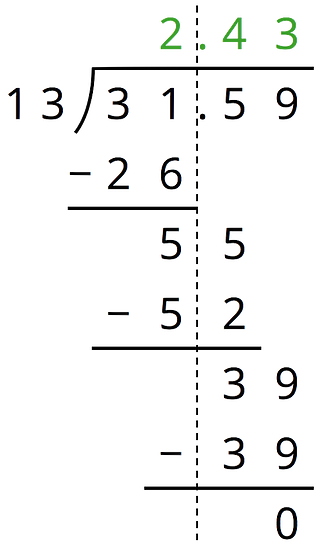
-
At the second step, Han subtracts 52 from 55. How do you know that these numbers represent tenths?
-
At the third step, Han subtracts 39 from 39. How do you know that these numbers represent hundredths?
-
Check that Han’s answer is correct by calculating the product of 2.43 and 13.
-
- Write two division expressions that have the same value as .
- Find the value of . Show your reasoning.
A bag of pennies weighs 5.1 kilogram. Each penny weighs 2.5 grams. About how many pennies are in the bag?
- 20
- 200
- 2,000
- 20,000
Find each difference. If you get stuck, consider drawing a diagram.
Plant B is inches tall. Plant C is inches tall. Complete the sentences and show your reasoning.
- Plant C is _______ times as tall as Plant B.
- Plant C is _______ inches ____________ (taller or shorter) than Plant B.
At a school, 460 of the students walk to school.
- The number of students who take public transit is 20% of the number of students who walk. How many students take public transit?
- The number of students who bike to school is 5% of the number of students who walk. How many students bike to school?
- The number of students who ride the school bus is 110% of the number of students who walk. How many students ride the school bus?