Open Up Resources Logo

Lesson 8Equal and Equivalent

Let's use diagrams to figure out which expressions are equivalent and which are just sometimes equal.

Learning Targets:

  • I can explain what it means for two expressions to be equivalent.
  • I can use a tape diagram to figure out when two expressions are equal.
  • I can use what I know about operations to decide whether two expressions are equivalent.

8.1 Algebra Talk: Solving Equations by Seeing Structure

Find a solution to each equation mentally.

  • 3 + x = 8
  • 10 = 12 - x
  • x^2 = 49
  • \frac13 x = 6

8.2 Using Diagrams to Show That Expressions are Equivalent

Here is a diagram of x+2 and 3x when x is 4. Notice that the two diagrams are lined up on their left sides.

Here is a diagram of x+2 and 3x when x is 4. Notice that the two diagrams are lined up on their left sides.

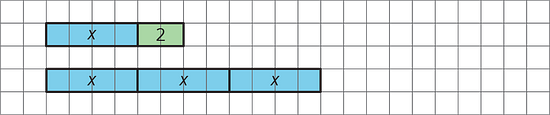
In each of your drawings below, line up the diagrams on one side.

  1. Draw a diagram of  x+2 , and a separate diagram of 3x , when x is 3.

    A blank grid with a height of 5 units and a length of 24 units.

  2. Draw a diagram of  x+2 , and a separate diagram of 3x , when x is 2.

    A blank grid with a height of 5 units and a length of 24 units.

  3. Draw a diagram of  x+2 , and a separate diagram of 3x , when x is 1.

    A blank grid with a height of 5 units and a length of 24 units.

  4. Draw a diagram of  x+2 , and a separate diagram of 3x , when x is 0.

    A blank grid with a height of 5 units and a length of 24 units.
  5. When are x+2 and 3x equal? When are they not equal? Use your diagrams to explain.
  6. Draw a diagram of x+3 , and a separate diagram of 3+x .
  7. When are x+3 and 3+x equal? When are they not equal? Use your diagrams to explain.

8.3 Identifying Equivalent Expressions

Here is a list of expressions. Find any pairs of expressions that are equivalent. If you get stuck, try reasoning with diagrams.

a+3

a+a+a

a \div \frac13

a \boldcdot 3

\frac13 a

3a

\frac{a}{3}

1a

a

3+a

Are you ready for more?

Below are four questions about equivalent expressions. For each one: 

  • Decide whether you think the expressions are equivalent.
  • Test your guess by choosing numbers for x (and y , if needed).
  1. Are \dfrac{x \boldcdot  x \boldcdot  x \boldcdot  x}{x} and x \boldcdot x \boldcdot x equivalent expressions?
  2. Are \dfrac{x + x + x + x}{x} and x + x + x equivalent expressions?
  3. Are 2(x+y) and 2x + 2y equivalent expressions?
  4. Are 2xy and 2x \boldcdot 2y equivalent expressions?

Lesson 8 Summary

We can use diagrams showing lengths of rectangles to see when expressions are equal. For example, the expressions x+9 and 4x are equal when x is 3, but are not equal for other values of x . 

Diagram showing different rectangle lengths is shown on a grid.

Sometimes two expressions are equal for only one particular value of their variable. Other times, they seem to be equal no matter what the value of the variable.

Expressions that are always equal for the same value of their variable are called equivalent expressions. However, it would be impossible to test every possible value of the variable. How can we know for sure that expressions are equivalent?

We use the meaning of operations and properties of operations to know that expressions are equivalent. Here are some examples:

  • x+3 is equivalent to 3+x because of the commutative property of addition.
  • 4\boldcdot {y} is equivalent to y\boldcdot 4 because of the commutative property of multiplication.
  • a+a+a+a+a is equivalent to 5\boldcdot {a} because adding 5 copies of something is the same as multiplying it by 5.
  • b\div3 is equivalent to b \boldcdot {\frac13} because dividing by a number is the same as multiplying by its reciprocal.

In the coming lessons, we will see how another property, the distributive property, can show that expressions are equivalent.

Glossary Terms

equivalent expressions

Equivalent expressions are always equal to each other. If the expressions have variables, they are equal whenever the same value is used for the variable in each expression.

For example, 3x+4x is equivalent to 5x+2x . No matter what value we use for x , these expressions are always equal. When x=3 , both expressions equal 21. When x=10 , both expressions equal 70.  

Lesson 8 Practice Problems

    1. Draw a diagram of x + 3 and a diagram of 2x when x is 1.

      A blank grid with a height of 5 units and a length of 24 units.

    2. Draw a diagram of x+3 and of 2x when x is 2.

      A blank grid with a height of 5 units and a length of 24 units.

    3. Draw a diagram of x+3 and of 2x when x is 3.

      A blank grid with a height of 5 units and a length of 24 units.

    4. Draw a diagram of x+3 and of 2x when x is 4.

      A blank grid with a height of 5 units and a length of 24 units.
    5. When are x+3 and 2x equal? When are they not equal? Use your diagrams to explain.
    1. Do 4x and 15+x have the same value when x is 5?
    2. Are 4x and 15+x equivalent expressions? Explain your reasoning.
    1. Check that 2b + b and 3b have the same value when b is 1, 2, and 3.
    1. Do 2b +b and 3b have the same value for all values of b ? Explain your reasoning.
    1. Are 2b+b and 3b equivalent expressions?

  4. 80% of x is equal to 100.

    1. Write an equation that shows the relationship of 80%, x , and 100.
    1. Use your equation to find x .

  5. For each story problem, write an equation to represent the problem and then solve the equation. Be sure to explain the meaning of any variables you use.

    1. Jada’s dog was 5\frac{1}{2} inches tall when it was a puppy. Now her dog is 14\frac{1}{2} inches taller than that. How tall is Jada’s dog now?
    2. Lin picked 9 \frac{3}{4} pounds of apples, which was 3 times the weight of the apples Andre picked. How many pounds of apples did Andre pick?