Lesson 15Shapes on the Coordinate Plane
Let’s use the coordinate plane to solve problems and puzzles.
Learning Targets:
- I can find the lengths of horizontal and vertical segments in the coordinate plane.
- I can plot polygons on the coordinate plane when I have the coordinates for the vertices.
15.1 Figuring Out The Coordinate Plane
- Draw a figure in the coordinate plane with at least three of following properties:
-
6 vertices
-
1 pair of parallel sides
-
At least 1 right angle
-
2 sides the same length
-
- Is your figure a polygon? Explain how you know.
15.2 Plotting Polygons
Here are the coordinates for four polygons. Move the slider to choose the polygon you want to plot. Move the points, in order, to their locations on the coordinate plane. Sketch each one before changing the slider.
-
Polygon 1:
-
Polygon 2:
-
Polygon 3:
-
Polygon 4:
Are you ready for more?
15.3 Four Quadrants of A-Maze-ing
-
The following diagram shows Andre’s route through a maze. He started from the lower right entrance.
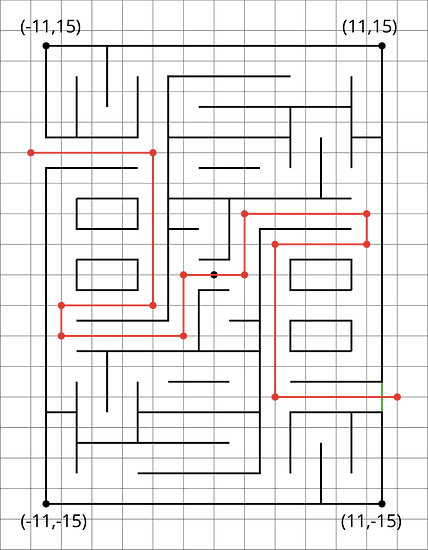
- What are the coordinates of the first two and the last two points of his route?
- How far did he walk from his starting point to his ending point? Show how you know.
-
Jada went into the maze and stopped at .
- Plot that point and other points that would lead her out of the maze (through the exit on the upper left side).
- How far from must she walk to exit the maze? Show how you know.
Lesson 15 Summary
We can use coordinates to find lengths of segments in the coordinate plane.

For example, we can find the perimeter of this polygon by finding the sum of its side lengths. Starting from and moving clockwise, we can see that the lengths of the segments are 6, 3, 3, 3, 3, and 6 units. The perimeter is therefore 24 units.
In general:
- If two points have the same -coordinate, they will be on the same vertical line, and we can find the distance between them.
- If two points have the same -coordinate, they will be on the same horizontal line, and we can find the distance between them.
Lesson 15 Practice Problems
The coordinates of a rectangle are , , and
- What is the length and width of this rectangle?
- What is the perimeter of the rectangle?
- What is the area of the rectangle?
Draw a square with one vertex on the point and a area of 25.
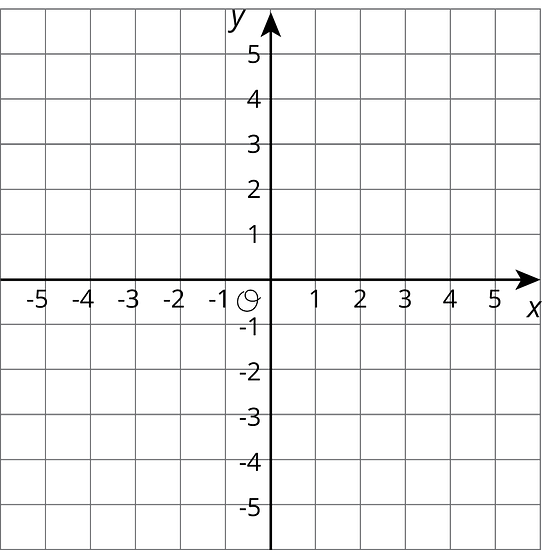
- Plot and connect the following points to form a polygon.

-
Find the perimeter of the polygon.
- Plot and connect the following points to form a polygon.
For each situation, select all the equations that represent it. Choose one equation and solve it.
-
Jada’s cat weighs 3.45 kg. Andre’s cat weighs 1.2 kg more than Jada’s cat. How much does Andre’s cat weigh?
-
Apples cost $1.60 per pound at the farmer’s market. They cost 1.5 times as much at the grocery store. How much do the apples cost per pound at the grocery store?
(1.5)y = 1.60
-