Open Up Resources Logo

Lesson 10Changing Scales in Scale Drawings

Let’s explore different scale drawings of the same actual thing.

Learning Targets:

  • Given a scale drawing, I can create another scale drawing that shows the same thing at a different scale.
  • I can use a scale drawing to find actual areas.

10.1 Appropriate Measurements

  1. If a student uses a ruler like this to measure the length of their foot, which choices would be appropriate measurements? Select all that apply. Be prepared to explain your reasoning.
    The ruler measures inches and centimeters. The inches are broken into eighths and the centimeters are broken into tenths.

    1. 9\frac14 inches

    2. 9\frac{5}{64} inches

    3. 23.47659 centimeters

    4. 23.5 centimeters

    5. 23.48 centimeters

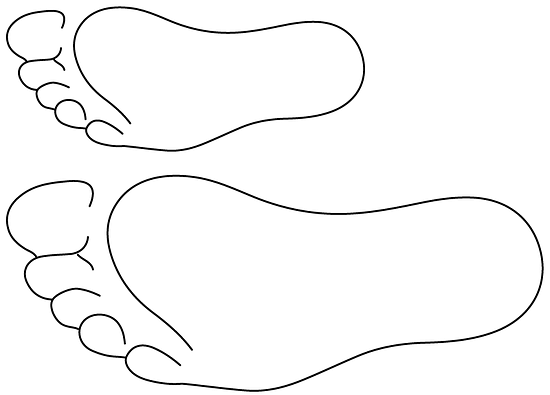
  2. Here is a scale drawing of an average seventh-grade student's foot next to a scale drawing of a foot belonging to the person with the largest feet in the world. Estimate the length of the larger foot.

    Image of two different sized feet

10.2 Same Plot, Different Drawings

Here is a map showing a plot of land in the shape of a right triangle.

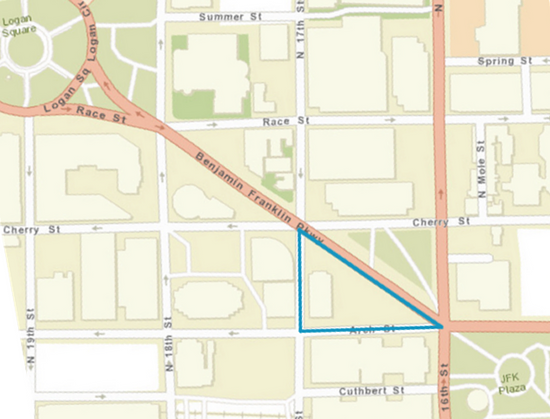
A map that shows a plot of land indicated by a right triangle.
“Logan Square map” by United States Census Bureau via American Fact Finder. Public Domain.
  1. Your teacher will assign you a scale to use. On centimeter graph paper, make a scale drawing of the plot of land. Make sure to write your scale on your drawing.
  2. What is the area of the triangle you drew? Explain or show your reasoning.
  3. How many square meters are represented by 1 square centimeter in your drawing?
  4. After everyone in your group is finished, order the scale drawings from largest to smallest. What do you notice about the scales when your drawings are placed in this order?

Are you ready for more?

Noah and Elena each make a scale drawing of the same triangular plot of land, using the following scales. Make a prediction about the size of each drawing. How would they compare to the scale drawings made by your group?

  1. Noah uses the scale 1 cm to 200 m.

  2. Elena uses the scale 2 cm to 25 m.

10.3 A New Drawing of the Playground

Here is a scale drawing of a playground. 

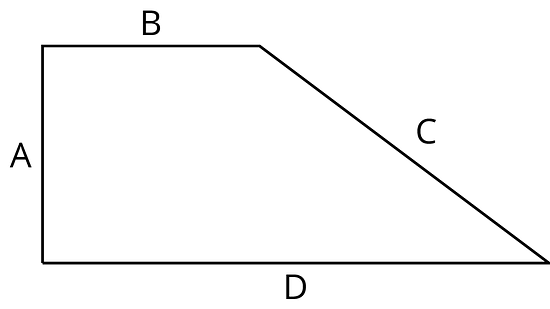
Trapezoid ABCD

The scale is 1 centimeter to 30 meters.

  1. Make another scale drawing of the same playground at a scale of 1 centimeter to 20 meters.
  2. How do the two scale drawings compare?

Lesson 10 Summary

Sometimes we have a scale drawing of something, and we want to create another scale drawing of it that uses a different scale. We can use the original scale drawing to find the size of the actual object. Then we can use the size of the actual object to figure out the size of our new scale drawing.

For example, here is a scale drawing of a park where the scale is 1 cm to 90 m.

A scale drawing of a park

The rectangle is 10 cm by 4 cm, so the actual dimensions of the park are 900 m by 360 m, because 10 \boldcdot 90 = 900 and 4 \boldcdot 90 = 360 .

Suppose we want to make another scale drawing of the park where the scale is 1 cm to 30 meters. This new scale drawing should be 30 cm by 12 cm, because 900 \div 30 = 30 and 360 \div 30 = 12 .

Another way to find this answer is to think about how the two different scales are related to each other. In the first scale drawing, 1 cm represented 90 m. In the new drawing, we would need 3 cm to represent 90 m. That means each length in the new scale drawing should be 3 times as long as it was in the original drawing. The new scale drawing should be 30 cm by 12 cm, because 3 \boldcdot 10 = 30 and 3 \boldcdot 4 = 12 .

Since the length and width are 3 times as long, the area of the new scale drawing will be 9 times as large as the area of the original scale drawing, because 3^2=9 .

Lesson 10 Practice Problems

  1. Here is a scale drawing of a swimming pool where 1 cm represents 1 m.

    A scale drawing of a rectangular swimming pool.
    1. How long and how wide is the actual swimming pool? 
    2. Will a scale drawing where 1 cm represents 2 m be larger or smaller than this drawing?
    3. Make a scale drawing of the swimming pool where 1 cm represents 2 m.

  2. A map of a park has a scale of 1 inch to 1,000 feet. Another map of the same park has a scale of 1 inch to 500 feet. Which map is larger? Explain or show your reasoning. 

  3. On a map with a scale of 1 inch to 12 feet, the area of a restaurant is 60 in2. Han says that the actual area of the restaurant is 720 ft2. Do you agree or disagree? Explain your reasoning.

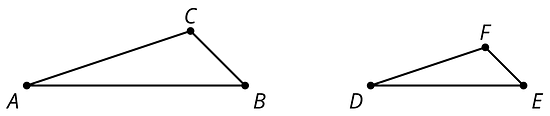
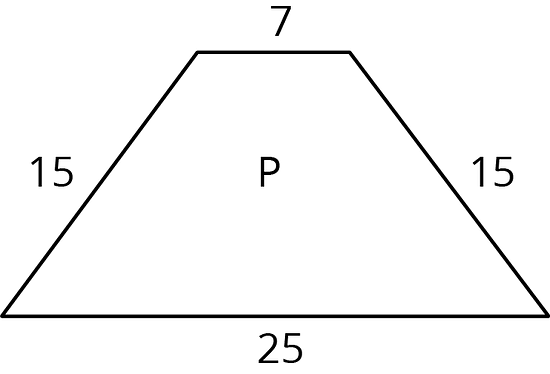
  4. If Quadrilateral Q is a scaled copy of Quadrilateral P created with a scale factor of 3, what is the perimeter of Q?

    A trapezoid labeled P. The parallel sides form the top and bottom of the shape. The length of the top side is labeled 7 units and the length of the bottom side is labeled 15 units. The two legs that join the two parallel sides together are each labeled 15 units

  5. Triangle DEF is a scaled copy of triangle ABC . For each of the following parts of triangle ABC , identify the corresponding part of triangle DEF .

    • angle ABC
    • angle BCA
    • segment AC
    • segment BA
    Two triangles labeled ABC and DEF. Triangle ABC has horizontal side AB with point B to the right of point A and point C is directly above side AB. Triangle DEF has horizontal side DE with point E to the right of point D and point F is directly above side DE.