Lesson 12Units in Scale Drawings
Let's use different scales to describe the same drawing.
Learning Targets:
- I can tell whether two scales are equivalent.
- I can write scales with units as scales without units.
12.1 Centimeters in a Mile
There are 2.54 cm in an inch, 12 inches in a foot, and 5,280 feet in a mile. Which expression gives the number of centimeters in a mile? Explain your reasoning.
12.2 Scales Card Sort
Your teacher will give you some cards with a scale on each card.
-
Sort the cards into sets of equivalent scales. Be prepared to explain how you know that the scales in each set are equivalent. Each set should have at least two cards.
-
Trade places with another group and check each other’s work. If you disagree about how the scales should be sorted, work to reach an agreement.
Pause here so your teacher can review your work.
- Next, record one of the sets with three equivalent scales and explain why they are equivalent.
12.3 The World’s Largest Flag
As of 2016, Tunisia holds the world record for the largest version of a national flag. It was almost as long as four soccer fields. The flag has a circle in the center, a crescent moon inside the circle, and a star inside the crescent moon.
- Complete the table. Explain or show your reasoning.
flag length flag height height of
crescent moonactual 396 m 99 m at 1 to 2,000 scale 13.2 cm -
Complete each scale with the value that makes it equivalent to the scale of 1 to 2,000. Explain or show your reasoning.
- 1 cm to ____________ cm
- 1 cm to ____________ m
- 1 cm to ____________ km
- 2 m to _____________ m
- 5 cm to ___________ m
- ____________ cm to 1,000 m
- ____________ mm to 20 m
-
- What is the area of the large flag?
- What is the area of the smaller flag?
- The area of the large flag is how many times the area of the smaller flag?
12.4 Pondering Pools
Your teacher will give you a floor plan of a recreation center.
- What is the scale of the floor plan if the actual side length of the square pool is 14 m? Express your answer both as a scale with units and without units.
- Find the actual area of the large rectangular pool. Show your reasoning.
- The kidney-shaped pool has an area of 3.2 cm2 on the drawing. What is its actual area? Explain or show your reasoning.
Are you ready for more?
- Square A is a scaled copy of Square B with scale factor 2. If the area of Square A is 10 units2, what is the area of Square B?
- Cube A is a scaled copy of Cube B with scale factor 2. If the volume of Cube A is 10 units3, what is the volume of Cube B?
- The four-dimensional Hypercube A is a scaled copy of Hypercube B with scale factor 2. If the “volume” of Hypercube A is 10 units4, what do you think the “volume” of Hypercube B is?
Lesson 12 Summary
Sometimes scales come with units, and sometimes they don’t. For example, a map of Nebraska may have a scale of 1 mm to 1 km. This means that each millimeter of distance on the map represents 1 kilometer of distance in Nebraska. The same scale without units is 1 to 1,000,000, which means that each unit of distance on the map represents 1,000,000 units of distance in Nebraska. This is true for any choice of unit.
To see that these two scales are equivalent, notice that there are 1,000 millimeters in 1 meter and 1,000 meters in 1 kilometer. This means there are or 1,000,000 millimeters in 1 kilometer. So the actual distances in Nebraska are 1,000,000 times as far as the distances on the map.
A scale tells us how a length on a drawing corresponds to an actual length, and it also tells us how an area on a drawing corresponds to an actual area.
For example, if 1 centimeter on a scale drawing represents 2 meters in actual distance, what does 1 square centimeter on the drawing represent in actual area? The square on the left shows a square with side lengths 1 cm, so its area is 1 square cm.

The square on the right shows the actual dimensions represented by the square on the left. Because each side length in the actual square is 2 m, the actual square has an area of or 4 square meters.
We can use this relationship to find the actual area of any region represented on this drawing. If a room has an area of 18 cm2 on the drawing, we know that it has an actual area of or 72 m2.
In general, if 1 unit on the drawing represents actual units, then one square unit on the drawing represents actual square units.
Lesson 12 Practice Problems
The Empire State Building in New York City is about 1,450 feet high (including the antenna at the top) and 400 feet wide. Andre wants to make a scale drawing of the front view of the Empire State Building on an -inch-by--inch piece of paper. Select a scale that you think is the most appropriate for the scale drawing. Explain your reasoning.
- 1 inch to 1 foot
- 1 inch to 100 feet
- 1 inch to 1 mile
- 1 centimeter to 1 meter
- 1 centimeter to 50 meters
- 1 centimeter to 1 kilometer
Elena finds that the area of a house on a scale drawing is 25 square inches. The actual area of the house is 2,025 square feet. What is the scale of the drawing?
Which of these scales are equivalent to 3 cm to 4 km? Select all that apply. Recall that 1 inch is 2.54 centimeters.
-
0.75 cm to 1 km
-
1 cm to 12 km
-
6 mm to 2 km
-
0.3 mm to 40 m
-
1 inch to 7.62 km
-
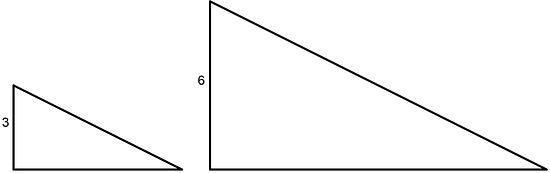
These two triangles are scaled copies of one another. The area of the smaller triangle is 9 square units. What is the area of the larger triangle? Explain or show how you know.
Water costs $1.25 per bottle. At this rate, what is the cost of:
- 10 bottles?
- 20 bottles?
- 50 bottles?
The first row of the table shows the amount of dish detergent and water needed to make a soap solution.
number of batches cups of water cups of detergent 1 6 1 2 3 4 -
Complete the table for 2, 3, and 4 batches.
-
How much water and detergent is needed for 8 batches? Explain your reasoning.
-