Open Up Resources Logo

Lesson 6Scaling and Area

Let's build scaled shapes and investigate their areas.

Learning Targets:

  • I can describe how the area of a scaled copy is related to the area of the original figure and the scale factor that was used.

6.1 Scaling a Pattern Block

Use the applets to explore the pattern blocks. Work with your group to build the scaled copies described in each question.

A parallelogram, triangle, and trapezoid
  1. How many blue rhombus blocks does it take to build a scaled copy of Figure A:

    1. Where each side is twice as long?

    2. Where each side is 3 times as long?

    3. Where each side is 4 times as long?

    open applet in presentation mode
  2. How many green triangle blocks does it take to build a scaled copy of Figure B:

    1. Where each side is twice as long?

    2. Where each side is 3 times as long?

    3. Using a scale factor of 4?

    open applet in presentation mode
  3. How many red trapezoid blocks does it take to build a scaled copy of Figure C:

    1. Using a scale factor of 2?

    2. Using a scale factor of 3?

    3. Using a scale factor of 4?

    open applet in presentation mode
  4. Make a prediction: How many blocks would it take to build scaled copies of these shapes using a scale factor of 5? Using a scale factor of 6? Be prepared to explain your reasoning.

6.2 Scaling More Pattern Blocks

Your teacher will assign your group one of these figures, each made with original-size blocks.

Three figures mad out of different shapes

  1. In the applet, move the slider to see a scaled copy of your assigned shape, using a scale factor of 2. Use the original-size blocks to build a figure to match it. How many blocks did it take?

  2. Explain why doubling the blocks was not enough to match the scaled copy, even though the scale factor was 2.

  3. Move the slider to see a scaled copy of your assigned shape using a scale factor of 3. Start building a figure with the original-size blocks to match it. Stop when you can tell for sure how many blocks it would take. Record your answer.

  4. Predict: How many blocks would it take to build scaled copies using scale factors 4, 5, and 6? Explain or show your reasoning.

  5. How is the pattern in this activity the same as the pattern you saw in the previous activity? How is it different?

  6. Discuss your answers with another group that worked on the same shape until you reach an agreement. Be prepared to share your reasoning with the class.

open applet in presentation mode
open applet in presentation mode
open applet in presentation mode

Are you ready for more?

  1. How many blocks do you think it would take to build a scaled copy of one yellow hexagon where each side is twice as long? Three times as long?

  2. Figure out a way to build these scaled copies. 

  3. Do you see a pattern for the number of blocks used to build these scaled copies? Explain your reasoning.

6.3 Area of Scaled Parallelograms and Triangles

  1. Your teacher will give you a figure with measurements in centimeters. What is the area of your figure? How do you know?
  2. Work with your partner to draw scaled copies of your figure, using each scale factor in the table. Complete the table with the measurements of your scaled copies.
    scale factor base (cm) height (cm) area (cm2)
    1
    2
    3
    \frac{1}{2}
    \frac{1}{3}
  3. Compare your results with a group that worked with a different figure. What is the same about your answers? What is different?
  4. If you drew scaled copies of your figure with the following scale factors, what would their areas be? Discuss your thinking. If you disagree, work to reach an agreement. Be prepared to explain your reasoning.
    scale factor area (cm2)
    5
    \frac{3}{5}

Lesson 6 Summary

Scaling affects lengths and areas differently. When we make a scaled copy, all original lengths are multiplied by the scale factor. If we make a copy of a rectangle with side lengths 2 units and 4 units using a scale factor of 3, the side lengths of the copy will be 6 units and 12 units, because 2\boldcdot 3 = 6 and 4\boldcdot 3 = 12 .

Two rectangles: The first rectangle has a horizontal length labeled 4 and vertical width labeled 2. The second rectangle has a horizontal length labeled 12 and vertical width labeled 6.

The area of the copy, however, changes by a factor of (scale factor)2. If each side length of the copy is 3 times longer than the original side length, then the area of the copy will be 9 times the area of the original, because 3\boldcdot 3 , or  3^2 , equals 9.

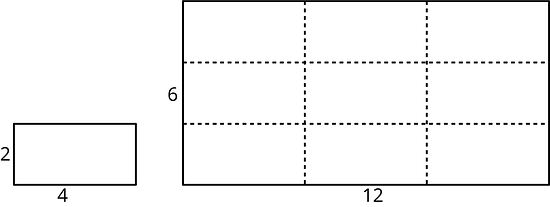
Two rectangles. The first rectangle has the vertical side labeled 2 and the horizontal side labeled 4. The second rectangle has the vertical side labeled 6 and the horizontal side labeled 12. Two horizontal dashed lines and 2 vertical dashed lines are drawn in the second rectangle dividing it into 9 identical smaller rectangles.

In this example, the area of the original rectangle is 8 units2 and the area of the scaled copy is 72 units2, because 9\boldcdot 8 = 72 . We can see that the large rectangle is covered by 9 copies of the small rectangle, without gaps or overlaps. We can also verify this by multiplying the side lengths of the large rectangle: 6\boldcdot 12=72 .

Lengths are one-dimensional, so in a scaled copy, they change by the scale factor. Area is two-dimensional, so it changes by the square of the scale factor. We can see this is true for a rectangle with length l and width w . If we scale the rectangle by a scale factor of s , we get a rectangle with length s\boldcdot l and width s\boldcdot w . The area of the scaled rectangle is  A = (s\boldcdot l) \boldcdot (s\boldcdot w) , so  A= (s^2) \boldcdot (l \boldcdot w) . The fact that the area is multiplied by the square of the scale factor is true for scaled copies of other two-dimensional figures too, not just for rectangles.

Lesson 6 Practice Problems

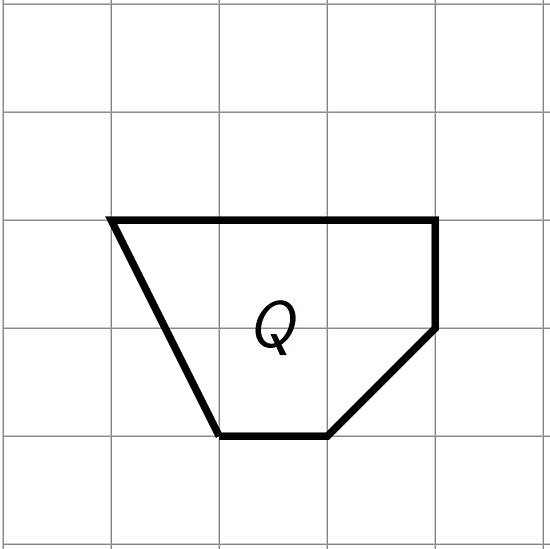
  1. On the grid, draw a scaled copy of Polygon Q using a scale factor of 2. Compare the perimeter and area of the new polygon to those of Q.

    A polygon aligned to a square grid is labeled Q. The shape is composed of 3 rectangles. The left part of the shape is 2 squares tall and 1 square wide. The next part of the shape is 3 squares tall and 2 squares wide. The next part of the shape begins 1 square up from the bottom of the shape and is 2 squares tall by 4 squares wide.

  2. A right triangle has an area of 36 square units.

    If you draw scaled copies of this triangle using the scale factors in the table, what will the areas of these scaled copies be? Explain or show your reasoning.

    scale factor area (units2)
    1 36
    2
    3
    5
    \frac12
    \frac23

  3. Diego drew a scaled version of a Polygon P and labeled it Q.

    A polygon aligned to a square grid labeled Q. The polygon is made up of 4 shapes, joined together along their edges. On the left is a right triangle with a base of 1 unit and a height of 2 units. To the right of the triangle is a 2 unit by 1 unit rectangle aligned with its 2 unit side next to the 2 unit side of the triangle. To the right of this is a 1 unit square, on top of a one-half unit triangle.

    If the area of Polygon P is 72 square units, what scale factor did Diego use to go from P to Q? Explain your reasoning.

  4. Here is an unlabeled polygon, along with its scaled copies Polygons A–D. For each copy, determine the scale factor. Explain how you know.

    An unlabeled four sided polygon with four different scale copies labeled A, B, C and D on a square grid. The unlabeled polygon has 4 sides, with a vertical heightof 2 on the left side. The height of the vertical side in each polygon is as follows: Polygon A: 1 unit. Polygon B: 4 units. Polygon C: 3 units. Polygon D: 2 units.

  5. Solve each equation mentally.

    1. \frac17\boldcdot x=1
    2. x \boldcdot \frac{1}{11}=1
    3. 1\div \frac{1}{5}=x