Open Up Resources Logo

Lesson 8Comparing Relationships with Equations

Let’s develop methods for deciding if a relationship is proportional.

Learning Targets:

  • I can decide if a relationship represented by an equation is proportional or not.

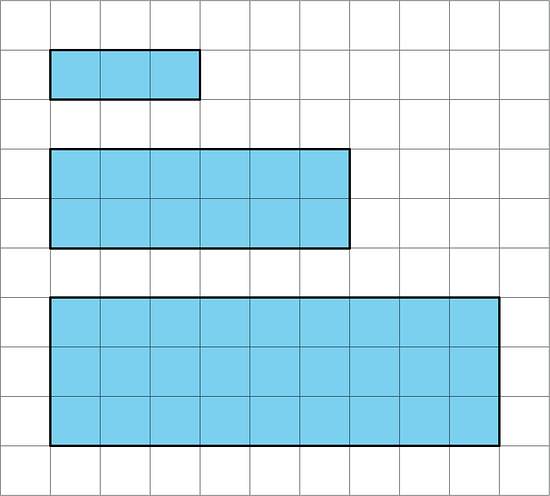
8.1 Notice and Wonder: Patterns with Rectangles

Three rectangles on a coordinate grid. The dimensions are as follows: Top rectangle, length 3 units; width 1 unit. Middle rectangle, length 6 units; width 2 units. Bottom rectangle, length 9 units, width 3 units.
Do you see a pattern? What predictions can you make about future rectangles in the set if your pattern continues?

8.2 More Conversions

The other day you worked with converting meters, centimeters, and millimeters. Here are some more unit conversions.

  1. Use the equation F =\frac95 C + 32 , where F represents degrees Fahrenheit and C represents degrees Celsius, to complete the table.
    temperature (^\circ\text{C}) temperature (^\circ\text{F})
    20
    4
    175
  2. Use the equation c = 2.54n , where c represents the length in centimeters and n represents the length in inches, to complete the table.
    length (in) length (cm)
    10
    8
    3 \frac12
  3. Are these proportional relationships? Explain why or why not.

8.3 Total Edge Length, Surface Area, and Volume

Here are some cubes with different side lengths. Complete each table. Be prepared to explain your reasoning.

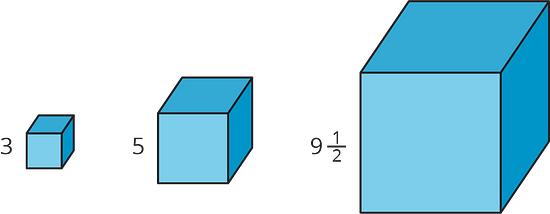
Three cubes of different sizes: first cube has side length 3, second cube side length 5, and thrid cube has side length 9 and 1/2
  1. How long is the total edge length of each cube?
side
length		 total
edge length
3
5
9\frac12
s
  1. What is the surface area of each cube?
side
length		 surface
area
3
5
9\frac12
s
  1. What is the volume of each cube?
side
length		 volume
3
5
9\frac12
s
  1. Which of these relationships is proportional? Explain how you know.

  2. Write equations for the total edge length E , total surface area A , and volume V of a cube with side length s .

Are you ready for more?

  1. A rectangular solid has a square base with side length \ell , height 8, and volume V . Is the relationship between \ell and V a proportional relationship?
  2. A different rectangular solid has length \ell , width 10, height 5, and volume V . Is the relationship between \ell and V a proportional relationship?
  3. Why is the relationship between the side length and the volume proportional in one situation and not the other?

8.4 All Kinds of Equations

Here are six different equations.

y = 4 + x

y = \frac{x}{4}

y = 4x

y = 4^{x}

y = \frac{4}{x}

y = x^{4}

  1. Predict which of these equations represent a proportional relationship.
  1. Complete each table using the equation that represents the relationship.
Six identical three column tables with 4 rows of data: The first column is labeled "x", the second column is labeled "y", and the third column is labeled "the fraction y over x". Row 1: x, 2. Row 2: x, 3. Row 3: x, 4. Row 4: x, 5. Each table has an equation above it, as follows: Table 1, Equation 1: y equals 4 + x; Table 2, Equation 2: y equals 4x; Table 3, Equation 3: y equals the fraction 4 over x; Table 4, Equation 4: y equals x the fraction x over 4; Table 5, Equation 5: y equals 4 to power x; Table 6, Equation 6: y equals x to the power 4;
  1. Do these results change your answer to the first question? Explain your reasoning.
  2. What do the equations of the proportional relationships have in common?

Lesson 8 Summary

If two quantities are in a proportional relationship, then their quotient is always the same. This table represents different values of a and b , two quantities that are in a proportional relationship.

a b \frac{b}{a}
20 100 5
3 15 5
11 55 5
1 5 5

Notice that the quotient of b and a is always 5. To write this as an equation, we could say \frac{b}{a}=5 . If this is true, then b=5a . (This doesn’t work if a=0 , but it works otherwise.)

If quantity y is proportional to quantity x , we will always see this pattern:  \frac{y}{x} will always have the same value. This value is the constant of proportionality, which we often refer to as k . We can represent this relationship with the equation \frac{y}{x} = k (as long as x is not 0) or y=kx .

Note that if an equation cannot be written in this form, then it does not represent a proportional relationship. 

Lesson 8 Practice Problems

  1. The relationship between a distance in yards ( y ) and the same distance in miles ( m ) is described by the equation y = 1760m .

    1. Find measurements in yards and miles for distances by filling in the table.
      distance measured in miles distance measured in yards
      1
      5
      3,520
      17,600
    2. Is there a proportional relationship between a measurement in yards and a measurement in miles for the same distance? Explain why or why not.

  2. Decide whether or not each equation represents a proportional relationship.

    1. The remaining length ( L ) of 120-inch rope after x inches have been cut off:  120-x = L
    2. The total cost ( t ) after 8% sales tax is added to an item's price ( p ):  1.08p = t
    3. The number of marbles each sister gets ( x ) when m marbles are shared equally among four sisters:  x = \frac{m}{4}
    4. The volume ( V ) of a rectangular prism whose height is 12 cm and base is a square with side lengths s cm:  V = 12s^2
    1. Use the equation y = \frac52 x to fill in the table.

      Is y proportional to x and y ? Explain why or why not.

      x y
      2
      3
      6
    2. Use the equation y = 3.2x+5 to fill in the table.

      Is y proportional to x and y ? Explain why or why not.

      x y
      1
      2
      4

  4. To transmit information on the internet, large files are broken into packets of smaller sizes. Each packet has 1,500 bytes of information. An equation relating packets to bytes of information is given by b = 1,\!500p where p represents the number of packets and b represents the number of bytes of information.

    1. How many packets would be needed to transmit 30,000 bytes of information?
    2. How much information could be transmitted in 30,000 packets?
    3. Each byte contains 8 bits of information. Write an equation to represent the relationship between the number of packets and the number of bits.