Open Up Resources Logo

Lesson 2Changing Temperatures

Let's add signed numbers.

Learning Targets:

  • I can use a number line to add positive and negative numbers.

2.1 Which One Doesn’t Belong: Arrows

Which pair of arrows doesn't belong?

  1. a number line
  2. a number line
  3. a number line
  4. a number line

2.2 Warmer and Colder

  1. Complete the table and draw a number line diagram for each situation.

    start ( ^\circ\text{C} ) change ( ^\circ\text{C} )  final ( ^\circ \text{C} ) addition equation
    a +40 10 degrees warmer +50 40 + 10 = 50
    b +40 5 degrees colder
    c +40 30 degrees colder
    d +40 40 degrees colder
    e +40 50 degrees colder
    1. A blank number line
    2. A blank number line
    3. A blank number line
    4. A blank number line
    5. A blank number line

  2. Complete the table and draw a number line diagram for each situation.

    start ( ^\circ\text{C} ) change ( ^\circ\text{C} ) final ( ^\circ\text{C} ) addition equation
    a -20 30 degrees warmer
    b -20 35 degrees warmer
    c -20 15 degrees warmer
    d -20 15 degrees colder
    1. A blank number line
    2. A blank number line
    3. A blank number line
    4. A blank number line

Are you ready for more?

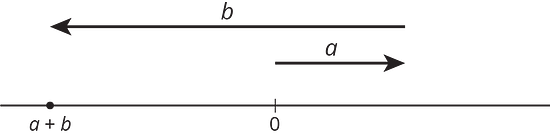
a number line

For the numbers a and b represented in the figure, which expression is equal to |a+b| ?

|a|+|b|

|a|-|b|

|b|-|a|

2.3 Winter Temperatures

  1. One winter day, the temperature in Houston is 8^\circ Celsius. Find the temperatures in these other cities. Explain or show your reasoning.
    1. In Orlando, it is 10^\circ warmer than it is in Houston.
    2. In Salt Lake City, it is 8^\circ colder than it is in Houston.
    3. In Minneapolis, it is 20^\circ colder than it is in Houston.
  2. In Fairbanks, it is 10^\circ colder than it is in Minneapolis. What is the temperature in Fairbanks?
  3. Use the thermometer applet to verify your answers and explore your own scenarios.
open applet in presentation mode

Lesson 2 Summary

If it is 42^\circ outside and the temperature increases by 7^\circ , then we can add the initial temperature and the change in temperature to find the final temperature.

42 + 7 = 49

If the temperature decreases by  7^\circ , we can either subtract 42-7 to find the final temperature, or we can think of the change as  \text-7^\circ . Again, we can add to find the final temperature.

42 + (\text-7) = 35

In general, we can represent a change in temperature with a positive number if it increases and a negative number if it decreases. Then we can find the final temperature by adding the initial temperature and the change. If it is 3^\circ and the temperature decreases by 7^\circ , then we can add to find the final temperature.

3+ (\text-7) = \text-4

We can represent signed numbers with arrows on a number line. We can represent positive numbers with arrows that start at 0 and points to the right. For example, this arrow represents +10 because it is 10 units long and it points to the right.

A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the left, and ends at negative 4.There is a solid dot indicated at 4.

We can represent negative numbers with arrows that start at 0 and point to the left. For example, this arrow represents -4 because it is 4 units long and it points to the left.

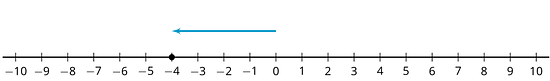
A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the left, and ends at negative 4.There is a solid dot indicated at 4.

To represent addition, we put the arrows “tip to tail.” So this diagram represents 3+5 :

A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the right, and ends at 3. A second arrow starts at 3, points to the right, and ends at 8. there is a solid dot indicated at 8.

And this represents 3 + (\text-5) :

A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the right, and ends at three. A second arrow starts at 3, points to the left, and ends at negative 2. There is a solid dot indicated at negative

Lesson 2 Practice Problems

    1. The temperature is -2 ^\circ \text{C} . If the temperature rises by 15 ^\circ \text{C} , what is the new temperature?
    2. At midnight the temperature is -6 ^\circ \text{C} . At midday the temperature is 9 ^\circ \text{C} . By how much did the temperature rise?

  2. Complete each statement with a number that makes the statement true.

    1. _____ < 7^\circ \text{C}
    2. _____ < \text- 3^\circ \text{C}
    3. \text- 0.8^\circ \text{C} < _____ < \text- 0.1^\circ \text{C}
    4. _____ > \text- 2^\circ \text{C}

  3. Draw a diagram to represent each of these situations. Then write an addition expression that represents the final temperature.

    1. The temperature was 80 ^\circ \text{F} and then fell  20 ^\circ \text{F} .
    2. The temperature was \text-13 ^\circ \text{F} and then rose 9 ^\circ \text{F} .
    3. The temperature was \text-5 ^\circ \text{F} and then fell  8 ^\circ \text{F} .

  4. Decide whether each table could represent a proportional relationship. If the relationship could be proportional, what would be the constant of proportionality?

    1. The number of wheels on a group of buses.

      number of buses number of wheels wheels per bus
      5 30
      8 48
      10 60
      15 90

    2. The number of wheels on a train.

      number of train cars number of wheels wheels per train car
      20 184
      30 264
      40 344
      50 424

  5. Noah was assigned to make 64 cookies for the bake sale. He made 125% of that number. 90% of the cookies he made were sold. How many of Noah's cookies were left after the bake sale?