Lesson 15Efficiently Solving Inequalities
Let’s solve more complicated inequalities.
Learning Targets:
- I can graph the solutions to an inequality on a number line.
- I can solve inequalities by solving a related equation and then checking which values are solutions to the original inequality.
15.1 Lots of Negatives
Here is an inequality: .
- Predict what you think the solutions on the number line will look like.
- Select all the values that are solutions to :
- 3
- -3
- 4
- -4
- 4.001
- -4.001
- Graph the solutions to the inequality on the number line:

15.2 Inequalities with Tables
-
Let's investigate the inequality .
-4 -3 -2 -1 0 1 2 3 4 -7 -5 -1 1 - Complete the table.
- For which values of is it true that ?
- For which values of is it true that ?
- Graph the solutions to on the number line:

-
Here is an inequality: .
- Predict which values of will make the inequality true.
-
Complete the table. Does it match your prediction?
-4 -3 -2 -1 0 1 2 3 4 -
Graph the solutions to on the number line:

-
Here is an inequality: .
- Predict which values of will make the inequality true.
-
Complete the table. Does it match your prediction?
-4 -3 -2 -1 0 1 2 3 4 - Graph the solutions to on the number line:

- How are the solutions to different from the solutions to ?
15.3 Which Side are the Solutions?
- Let’s investigate .
- Solve .
- Is true when is 0? What about when is 7? What about when is -7?
- Graph the solutions to on the number line.

- Let's investigate .
- Solve .
- Is true when is 0?
-
Graph the solutions to on the number line.

- Solve the inequality and graph the solutions on the number line.

- Solve the inequality and graph the solutions on the number line.

Are you ready for more?
Write at least three different inequalities whose solution is . Find one with on the left side that uses a .
Lesson 15 Summary
Here is an inequality: . The solution to this inequality is all the values you could use in place of to make the inequality true.
In order to solve this, we can first solve the related equation to get the solution . That means 2 is the boundary between values of that make the inequality true and values that make the inequality false.
To solve the inequality, we can check numbers greater than 2 and less than 2 and see which ones make the inequality true.
Let’s check a number that is greater than 2: . Replacing with 5 in the inequality, we get or just . This is true, so is a solution. This means that all values greater than 2 make the inequality true. We can write the solutions as and also represent the solutions on a number line:
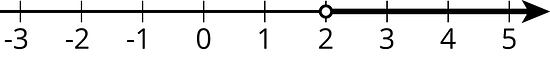
Notice that 2 itself is not a solution because it's the value of that makes equal to 18, and so it does not make true.
For confirmation that we found the correct solution, we can also test a value that is less than 2. If we test , we get or just . This is false, so and all values of that are less than 2 are not solutions.
Lesson 15 Practice Problems
- Consider the inequality .
- Predict which values of will make the inequality true.
- Complete the table to check your prediction.
-4 -3 -2 -1 0 1 2 3 4
- Consider the inequality .
- Predict which values of will make it true.
- Complete the table to check your prediction.
-4 -3 -2 -1 0 1 2 3 4
- Consider the inequality .
Diego is solving the inequality . He solves the equation and gets . What is the solution to the inequality?
- Solve the inequality , and graph the solution on a number line.
Select all values of that make the inequality true.
- -3.9
- 4
- -4.01
- -4
- 4.01
- 3.9
- 0
- -7
Draw the solution set for each of the following inequalities.
-
The price of a pair of earrings is $22 but Priya buys them on sale for $13.20.
- By how much was the price discounted?
- What was the percentage of the discount?