Lesson 19Expanding and Factoring
Let's use the distributive property to write expressions in different ways.
Learning Targets:
- I can organize my work when I use the distributive property.
- I can use the distributive property to rewrite expressions with positive and negative numbers.
- I understand that factoring and expanding are words used to describe using the distributive property to write equivalent expressions.
19.1 Number Talk: Parentheses
Find the value of each expression mentally.
19.2 Factoring and Expanding with Negative Numbers
In each row, write the equivalent expression. If you get stuck, use a diagram to organize your work. The first row is provided as an example. Diagrams are provided for the first three rows.

| factored | expanded |
|---|---|
Are you ready for more?
Expand to create an equivalent expression that uses the fewest number of terms: . If we wrote a new expression following the same pattern so that there were 20 sets of parentheses, how could it be expanded into an equivalent expression that uses the fewest number of terms?
Lesson 19 Summary
We can use properties of operations in different ways to rewrite expressions and create equivalent expressions. We have already seen that we can use the distributive property to expand an expression, for example . We can also use the distributive property in the other direction and factor an expression, for example .
We can organize the work of using distributive property to rewrite the expression . In this case we know the product and need to find the factors.
The terms of the product go inside:
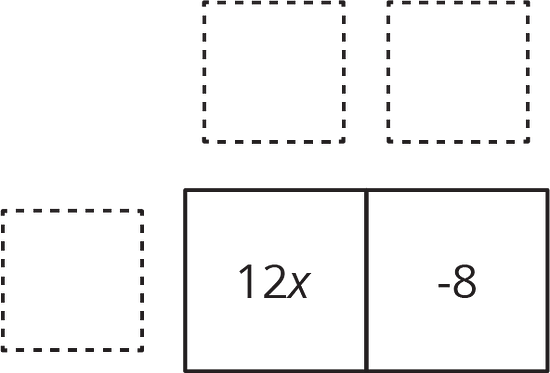
We look at the expressions and think about a factor they have in common. and each have a factor of 4. We place the common factor on one side of the large rectangle:
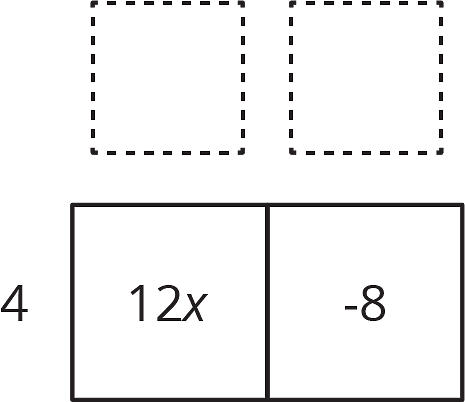
Now we think: "4 times what is 12?" "4 times what is -8?" and write the other factors on the other side of the rectangle:

So, is equivalent to .
Lesson 19 Practice Problems
- Expand to write an equivalent expression:
- Factor to write an equivalent expression:
Lin missed math class on the day they worked on expanding and factoring. Kiran is helping Lin catch up.
- Lin understands that expanding is using the distributive property, but she doesn’t understand what factoring is or why it works. How can Kiran explain factoring to Lin?
- Lin asks Kiran how the diagrams with boxes help with factoring. What should Kiran tell Lin about the boxes?
- Lin asks Kiran to help her factor the expression . How can Kiran use this example to Lin understand factoring?
Complete the equation with numbers that makes the expression on the right side of the equal sign equivalent to the expression on the left side.
Elena makes her favorite shade of purple paint by mixing 3 cups of blue paint, cups of red paint, and of a cup of white paint. Elena has of a cup of white paint.
- Assuming she has enough red paint and blue paint, how much purple paint can Elena make?
- How much blue paint and red paint will Elena need to use with the of a cup of white paint?
Solve each equation.
Select all the inequalities that have the same solutions as .