Lesson 6Distinguishing between Two Types of Situations
Let’s think about equations with and without parentheses and the kinds of situations they describe.
Learning Targets:
- I understand the similarities and differences between the two main types of equations we are studying in this unit.
- When I have a situation or a tape diagram, I can represent it with an equation.
6.1 Which One Doesn’t Belong: Seeing Structure
Which equation doesn’t belong?
6.2 Categories of Equations Card Sort
Be prepared to explain the meaning of your new categories.
6.3 Even More Situations, Diagrams, and Equations

Story 1: Lin had 90 flyers to hang up around the school. She gave 12 flyers to each of three volunteers. Then she took the remaining flyers and divided them up equally between the three volunteers.
Story 2: Lin had 90 flyers to hang up around the school. After giving the same number of flyers to each of three volunteers, she had 12 left to hang up by herself.
- Which diagram goes with which story? Be prepared to explain your reasoning.
- In each diagram, what part of the story does the variable represent?
- Write an equation corresponding to each story. If you get stuck, use the diagram.
- Find the value of the variable in the story.
Are you ready for more?
A tutor is starting a business. In the first year, they start with 5 clients and charge $10 per week for an hour of tutoring with each client. For each year following, they double the number of clients and the number of hours each week. Each new client will be charged 150% of the charges of the clients from the previous year.
- Organize the weekly earnings for each year in a table.
- Assuming a full-time week is 40 hours per week, how many years will it take to reach full time and how many new clients will be taken on that year?
- After reaching full time, what is the tutor’s annual salary if they take 2 weeks of vacation?
- Is there another business model you’d recommend for the tutor? Explain your reasoning.
Lesson 6 Summary
In this unit, we encounter two main types of situations that can be represented with an equation. Here is an example of each type:
-
After adding 8 students to each of 6 same-sized teams, there were 72 students altogether.
-
After adding an 8-pound box of tennis rackets to a crate with 6 identical boxes of ping pong paddles, the crate weighed 72 pounds.
The first situation has all equal parts, since additions are made to each team. An equation that represents this situation is , where represents the original number of students on each team. Eight students were added to each group, there are 6 groups, and there are a total of 72 students.
In the second situation, there are 6 equal parts added to one other part. An equation that represents this situation is , where represents the weight of a box of ping pong paddles, there are 6 boxes of ping pong paddles, there is an additional box that weighs 8 pounds, and the crate weighs 72 pounds altogether.
In the first situation, there were 6 equal groups, and 8 students added to each group. .
In the second situation, there were 6 equal groups, but 8 more pounds in addition to that. .
Lesson 6 Practice Problems
A school ordered 3 large boxes of board markers. After giving 15 markers to each of 3 teachers, there were 90 markers left. The diagram represents the situation. How many markers were originally in each box?
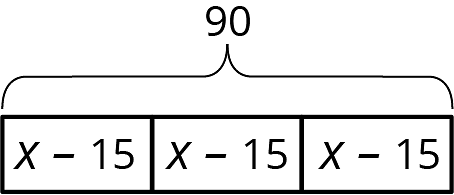
The diagram can be represented by the equation . Explain where you can see the 6 in the diagram.

Elena walked 20 minutes more than Lin. Jada walked twice as long as Elena. Jada walked for 90 minutes. The equation describes this situation. Match each amount in the story with the expression that represents it.
- 90
- The number of minutes that Jada walked
- The number of minutes that Elena walked
- The number of minutes that Lin walked
Match each equation to a story. (Two of the stories match the same equation.)
- Jada’s teacher fills a travel bag with 5 copies of a textbook. The weight of the bag and books is 17 pounds. The empty travel bag weighs 3 pounds. How much does each book weigh?
- A piece of scenery for the school play is in the shape of a 5-foot-long rectangle. The designer decides to increase the length. There will be 3 identical rectangles with a total length of 17 feet. By how much did the designer increase the length of each rectangle?
- Elena spends $17 and buys a $3 book and a bookmark for each of her 5 cousins. How much does each bookmark cost?
- Noah packs up bags at the food pantry to deliver to families. He packs 5 bags that weigh a total of 17 pounds. Each bag contains 3 pounds of groceries and a packet of papers with health-related information. How much does each packet of papers weigh?
- Andre has 3 times as many pencils as Noah and 5 pens. He has 17 pens and pencils all together. How many pencils does Noah have?