Lesson 10Designing Simulations
Let’s simulate some real-life scenarios.
Learning Targets:
- I can design a simulation to estimate the probability of a multi-step real-world situation.
10.1 Number Talk: Division
Find the value of each expression mentally.
10.2 Breeding Mice
A scientist is studying the genes that determine the color of a mouse’s fur. When two mice with brown fur breed, there is a 25% chance that their offspring will have white fur. For the experiment to continue, the scientist needs at least 2 out of 5 of the offspring to have white fur.
To simulate this situation, you can flip two coins at the same time for each offspring. If you don't have coins, you can use this applet.
- If both coins land heads up, it represents a mouse with white fur.
- Any other result represents a mouse with brown fur.
-
Have each person in the group simulate a litter of 5 offspring and record their results. Next, determine whether at least 2 of the offspring have white fur.
offspring 1 offspring 2 offspring 3 offspring 4 offspring 5 Do at least 2 have white fur? person 1’s simulation person 2’s simulation person 3’s simulation - Estimate the probability that the scientist’s experiment will be able to continue.
- How could you improve your estimate?
Are you ready for more?
For a certain pair of mice, the genetics show that each offspring has a probability of that they will be albino. Describe a simulation you could use that would estimate the probability that at least 2 of the 5 offspring are albino.
10.3 Designing Simulations
Your teacher will give your group a paper describing a situation.
- Design a simulation that you could use to estimate a probability. Show your thinking. Organize it so it can be followed by others.
- Explain how you used the simulation to answer the questions posed in the situation.
Lesson 10 Summary
Many real-world situations are difficult to repeat enough times to get an estimate for a probability. If we can find probabilities for parts of the situation, we may be able to simulate the situation using a process that is easier to repeat.
For example, if we know that each egg of a fish in a science experiment has a 13% chance of having a mutation, how many eggs do we need to collect to make sure we have 10 mutated eggs? If getting these eggs is difficult or expensive, it might be helpful to have an idea about how many eggs we need before trying to collect them.

We could simulate this situation by having a computer select random numbers between 1 and 100. If the number is between 1 and 13, it counts as a mutated egg. Any other number would represent a normal egg. This matches the 13% chance of each fish egg having a mutation.
We could continue asking the computer for random numbers until we get 10 numbers that are between 1 and 13. How many times we asked the computer for a random number would give us an estimate of the number of fish eggs we would need to collect.
To improve the estimate, this entire process should be repeated many times. Because computers can perform simulations quickly, we could simulate the situation 1,000 times or more.
Lesson 10 Practice Problems
A rare and delicate plant will only produce flowers from 10% of the seeds planted. To see if it is worth planting 5 seeds to see any flowers, the situation is going to be simulated. Which of these options is the best simulation? For the others, explain why it is not a good simulation.
- Another plant can be genetically modified to produce flowers 10% of the time. Plant 30 groups of 5 seeds each and wait 6 months for the plants to grow and count the fraction of groups that produce flowers.
- Roll a standard number cube 5 times. Each time a 6 appears, it represents a plant producing flowers. Repeat this process 30 times and count the fraction of times at least one number 6 appears.
- Have a computer produce 5 random digits (0 through 9). If a 9 appears in the list of digits, it represents a plant producing flowers. Repeat this process 300 times and count the fraction of times at least one number 9 appears.
- Create a spinner with 10 equal sections and mark one of them “flowers.” Spin the spinner 5 times to represent the 5 seeds. Repeat this process 30 times and count the fraction of times that at least 1 “flower” was spun.
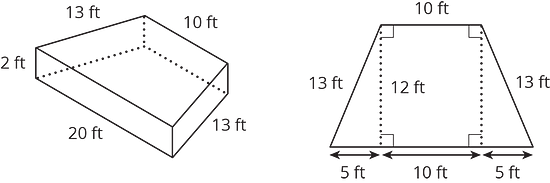
The figure on the left is a trapezoidal prism. The figure on the right represents its base. Find the volume of this prism.
Jada and Elena learned that 8% of students have asthma. They want to know the probability that in a team of 4 students, at least one of them has asthma. To simulate this, they put 25 slips of paper in a bag. Two of the slips say “asthma.” Next, they take four papers out of the bag and record whether at least one of them says “asthma.” They repeat this process 15 times.
-
Jada says they could improve the accuracy of their simulation by using 100 slips of paper and marking 8 of them.
-
Elena says they could improve the accuracy of their simulation by conducting 30 trials instead of 15.
-
Do you agree with either of them? Explain your reasoning.
-
Describe another method of simulating the same scenario.
-
Match each expression in the first list with an equivalent expression from the second list.