Lesson 2Chance Experiments
Let’s investigate chance.
Learning Targets:
- I can describe the likelihood of events using the words impossible, unlikely, equally likely as not, likely, or certain.
- I can tell which event is more likely when the chances of different events are expressed as fractions, decimals, or percentages.
2.1 Which is More Likely?
Which is more likely to happen?
-
When reaching into a dark closet and pulling out one shoe from a pile of 20 pairs of shoes, you pull out a left shoe.
-
When listening to a playlist—which has 5 songs on it—in shuffle mode, the first song on the playlist plays first.
2.2 How Likely Is It?
-
Label each event with one of these options:
impossible, unlikely, equally likely as not, likely, certain
- You will win grand prize in a raffle if you purchased 2 out of the 100 tickets.
- You will wait less than 10 minutes before ordering at a fast food restaurant.
- You will get an even number when you roll a standard number cube.
- A four-year-old child is over 6 feet tall.
- No one in your class will be late to class next week.
- The next baby born at a hospital will be a boy.
- It will snow at our school on July 1.
- The sun will set today before 11:00 p.m.
- Spinning this spinner will result in green.
- Spinning this spinner will result in yellow.
-
Discuss your answers to the previous question with your partner. If you disagree, work to reach an agreement.
- Invent another situation for each label, for a total of 5 more events.
2.3 Take a Chance
This applet displays a random number from 1 to 6, like a number cube. With a partner, you will play a game of chance.
-
In the first round, one of you will score on an even roll and one of you will score on an odd roll. You decide that first.
-
In the second round, the winner of round one will score on numbers , and the other player will score on numbers .
-
Each round is ten rolls. Be sure to turn on "History" after your first roll and wait for it to update before rolling again.
- When each player had three numbers, did one of them usually win?
- When one player had four numbers, did you expect them to usually win? Explain your reasoning.
Are you ready for more?
On a game show, there are 3 closed doors. One door has a prize behind it. The contestant chooses one of the doors. The host of the game show, who knows where the prize is located, opens one of the other doors which does not have the prize. The contestant can choose to stay with their first choice or switch to the remaining closed door.
- Do you think it matters if the contestant switches doors or stays?
- Practice playing the game with your partner and record your results. Whoever is the host starts each round by secretly deciding which door has the prize.
- Play 20 rounds where the contestant always stays with their first choice.
- Play 20 more rounds where the contestant always switches doors.
- Did the results from playing the game change your answer to the first question? Explain.
2.4 Card Sort: Likelihood
-
Your teacher will give you some cards that describe events. Order the events from least likely to most likely.
-
After ordering the first set of cards, pause here so your teacher can review your work. Then, your teacher will give you a second set of cards.
-
Add the new set of cards to the first set so that all of the cards are ordered from least likely to most likely.
Lesson 2 Summary
A chance experiment is something that happens where the outcome is unknown. For example, if we flip a coin, we don’t know if the result will be a head or a tail. An outcome of a chance experiment is something that can happen when you do a chance experiment. For example, when you flip a coin, one possible outcome is that you will get a head. An event is a set of one or more outcomes.
We can describe events using these phrases:
- Impossible
- Unlikely
- Equally likely as not
- Likely
- Certain
For example, if you flip a coin:
- It is impossible that the coin will turn into a bottle of ketchup.
- It is unlikely the coin will land on its edge.
- It is equally likely as not that you will get a tail.
- It is likely that you will get a head or a tail.
- It is certain that the coin will land somewhere.
The probability of an event is a measure of the likelihood that an event will occur. We will learn more about probabilities in the lessons to come.
Glossary Terms
A chance experiment is something you can do over and over again, and you don’t know what will happen each time.
For example, each time you spin the spinner, it could land on red, yellow, blue, or green.
An event is a set of one or more outcomes in a chance experiment. For example, if we roll a number cube, there are six possible outcomes.
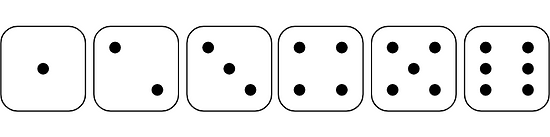
Examples of events are “rolling a number less than 3,” “rolling an even number,” or “rolling a 5.”
An outcome of a chance experiment is one of the things that can happen when you do the experiment. For example, the possible outcomes of tossing a coin are heads and tails.
Lesson 2 Practice Problems
The likelihood that Han makes a free throw in basketball is 60%. The likelihood that he makes a 3-point shot is 0.345. Which event is more likely, Han making a free throw or making a 3-point shot? Explain your reasoning.
Different events have the following likelihoods. Sort them from least to greatest:
- 60%
- 8 out of 10
- 0.37
- 20%
There are 25 prime numbers between 1 and 100. There are 46 prime numbers between 1 and 200. Which situation is more likely? Explain your reasoning.
- A computer produces a random number between 1 and 100 that is prime.
-
A computer produces a random number between 1 and 200 that is prime.
It takes cups of cheese, cups of olives, and cups of sausage to make a signature pizza. How much of each ingredient is needed to make 10 pizzas? Explain or show your reasoning.
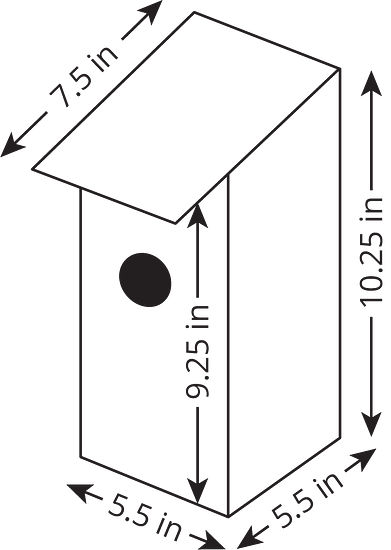
Here is a diagram of a birdhouse Elena is planning to build. (It is a simplified diagram, since in reality, the sides will have a thickness.) About how many square inches of wood does she need to build this birdhouse?
Select all the situations where knowing the surface area of an object would be more useful than knowing its volume.
- Placing an order for tiles to replace the roof of a house.
- Estimating how long it will take to clean the windows of a greenhouse.
- Deciding whether leftover soup will fit in a container.
- Estimating how long it will take to fill a swimming pool with a garden hose.
- Calculating how much paper is needed to manufacture candy bar wrappers.
- Buying fabric to sew a couch cover.
- Deciding whether one muffin pan is enough to bake a muffin recipe.