Lesson 10Composing Figures
Let’s use reasoning about rigid transformations to find measurements without measuring.
Learning Targets:
- I can find missing side lengths or angle measures using properties of rigid transformations.
10.1 Angles of an Isosceles Triangle
Here is a triangle.
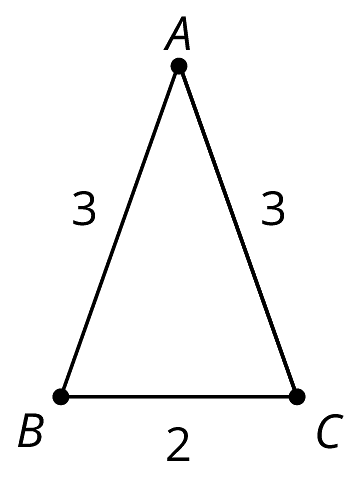
- Reflect triangle over line . Label the image of as .
- Rotate triangle around so that matches up with .
-
What can you say about the measures of angles and ?
10.2 Triangle Plus One
Here is triangle .

-
Draw midpoint of side .
-
Rotate triangle 180 degrees using center to form triangle . Draw and label this triangle.
-
What kind of quadrilateral is ? Explain how you know.
Are you ready for more?
In the activity, we made a parallelogram by taking a triangle and its image under a 180-degree rotation around the midpoint of a side. This picture helps you justify a well-known formula for the area of a triangle. What is the formula and how does the figure help justify it?
10.3 Triangle Plus Two
The picture shows 3 triangles. Triangle 2 and Triangle 3 are images of Triangle 1 under rigid transformations.
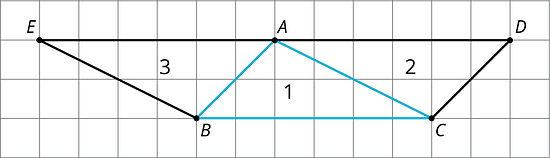
-
Describe a rigid transformation that takes Triangle 1 to Triangle 2. What points in Triangle 2 correspond to points , , and in the original triangle?
-
Describe a rigid transformation that takes Triangle 1 to Triangle 3. What points in Triangle 3 correspond to points , , and in the original triangle?
-
Find two pairs of line segments in the diagram that are the same length, and explain how you know they are the same length.
-
Find two pairs of angles in the diagram that have the same measure, and explain how you know they have the same measure.
10.4 Triangle ONE Plus
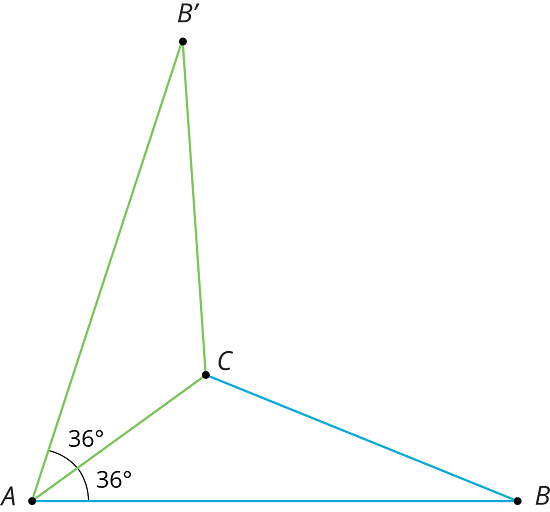
Here is isosceles triangle . Its sides and have equal lengths. Angle is 30 degrees. The length of is 5 units.
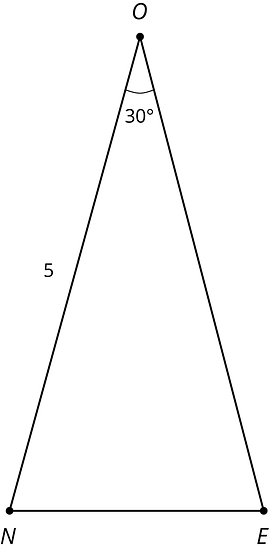
-
Reflect triangle across segment . Label the new vertex .
-
What is the measure of angle ?
-
What is the measure of angle ?
-
Reflect triangle across segment . Label the point that corresponds to as .
-
How long is ? How do you know?
-
What is the measure of angle ?
-
If you continue to reflect each new triangle this way to make a pattern, what will the pattern look like?
Lesson 10 Summary
Earlier, we learned that if we apply a sequence of rigid transformations to a figure, then corresponding sides have equal length and corresponding angles have equal measure. These facts let us figure out things without having to measure them!
For example, here is triangle .
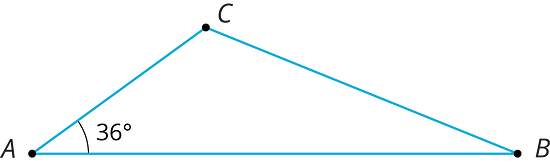
We can reflect triangle across side to form a new triangle:
Because points and are on the line of reflection, they do not move. So the image of triangle is . We also know that:
- Angle measures because it is the image of angle .
- Segment has the same length as segment .
When we construct figures using copies of a figure made with rigid transformations, we know that the measures of the images of segments and angles will be equal to the measures of the original segments and angles.
Lesson 10 Practice Problems
Here is the design for the flag of Trinidad and Tobago.

“The Flag of Trinidad and Tobago” via Wikimedia Commons. Public Domain. Describe a sequence of translations, rotations, and reflections that take the lower left triangle to the upper right triangle.
Here is a picture of an older version of the flag of Great Britain. There is a rigid transformation that takes Triangle 1 to Triangle 2, another that takes Triangle 1 to Triangle 3, and another that takes Triangle 1 to Triangle 4.

“Flag of Great Britain (1707–1800)” by Hoshi via Wikimedia Commons. Public Domain. - Measure the lengths of the sides in Triangles 1 and 2. What do you notice?
- What are the side lengths of Triangle 3? Explain how you know.
- Do all eight triangles in the flag have the same area? Explain how you know.
- Which of the lines in the picture is parallel to line ? Explain how you know.
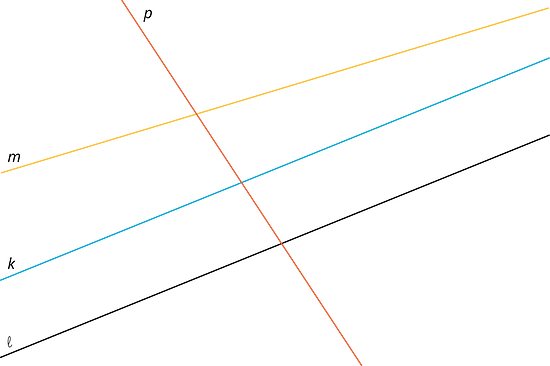
- Explain how to translate, rotate or reflect line to obtain line .
- Explain how to translate, rotate or reflect line to obtain line .
- Which of the lines in the picture is parallel to line ? Explain how you know.
Point has coordinates . After a translation 4 units left, a reflection across the -axis, and a translation 2 units down, what are the coordinates of the image?
Here is triangle :
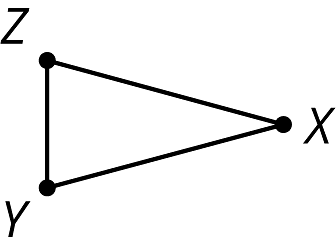
Draw these three rotations of triangle together.
- Rotate triangle 90 degrees clockwise around .
- Rotate triangle 180 degrees around .
- Rotate triangle 270 degrees clockwise around .