Lesson 2Naming the Moves
Let’s be more precise about describing moves of figures in the plane.
Learning Targets:
- I can identify corresponding points before and after a transformation.
- I know the difference between translations, rotations, and reflections.
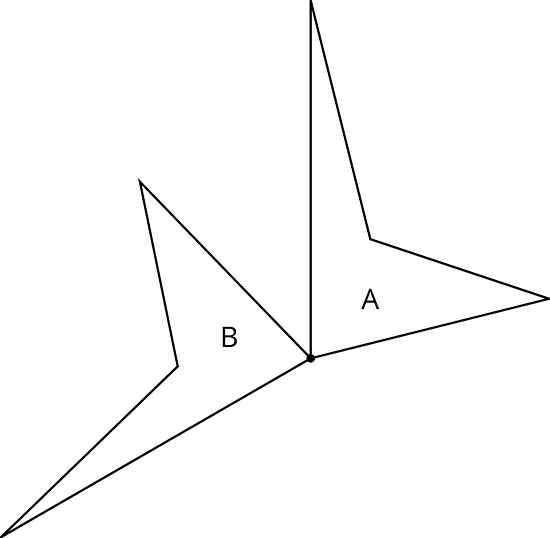
2.1 A Pair of Quadrilaterals
Quadrilateral A can be rotated into the position of Quadrilateral B.
2.2 How Did You Make That Move?
Here is another set of dance moves.
-
Describe each move or say if it is a new move.
-
Frame 1 to Frame 2.
-
Frame 2 to Frame 3.
-
Frame 3 to Frame 4.
-
Frame 4 to Frame 5.
-
Frame 5 to Frame 6.
-
-
How would you describe the new move?
2.3 Move Card Sort
Your teacher will give you a set of cards. Sort the cards into categories according to the type of move they show. Be prepared to describe each category and why it is different from the others. You can explore the applets below to see the ways the images move.
Drag the red point. Explore how the image changes.
Click on the box to show the transformed image.
Move the yellow points and the red segment to see how the image changes.
Lesson 2 Summary
Here are the moves we have learned about so far:
-
A translation slides a figure without turning it. Every point in the figure goes the same distance in the same direction. For example, Figure A was translated down and to the left, as shown by the arrows. Figure B is a translation of Figure A.

-
A rotation turns a figure about a point, called the center of the rotation. Every point on the figure goes in a circle around the center and makes the same angle. The rotation can be clockwise, going in the same direction as the hands of a clock, or counterclockwise, going in the other direction. For example, Figure A was rotated clockwise around its bottom vertex. Figure C is a rotation of Figure A.

-
A reflection places points on the opposite side of a reflection line. The mirror image is a backwards copy of the original figure. The reflection line shows where the mirror should stand. For example, Figure A was reflected across the dotted line. Figure D is a reflection of Figure A.
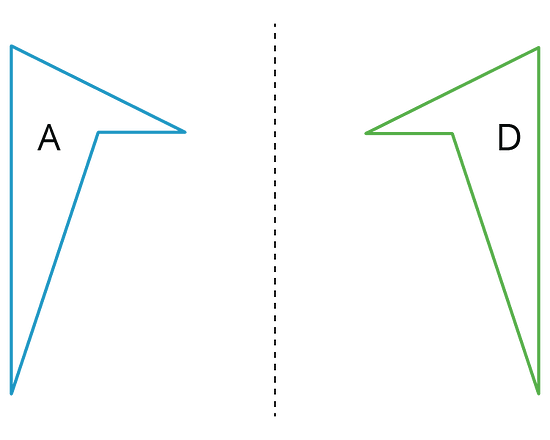
We use the word image to describe the new figure created by moving the original figure. If one point on the original figure moves to another point on the new figure, we call them corresponding points.
Glossary Terms
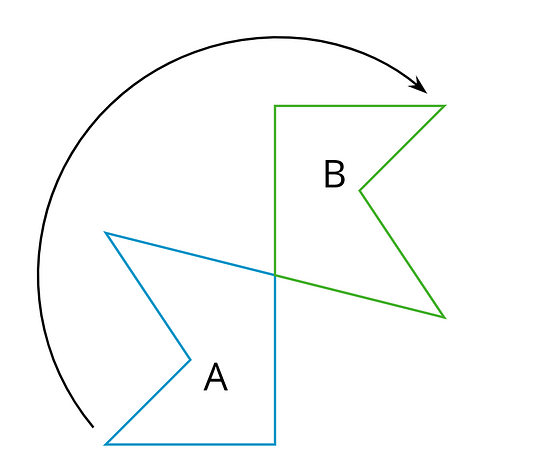
Clockwise means to turn in the same direction as the hands of a clock. It is a turn to the right. This diagram shows Figure A turned clockwise to make Figure B.
When part of an original figure matches up with part of a copy, we call them corresponding parts. These could be points, segments, angles, or distances.
For example, point in the first triangle corresponds to point in the second triangle.
Segment corresponds to segment .
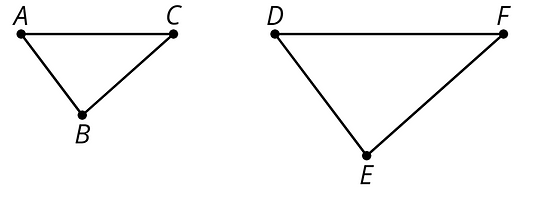
Counterclockwise means to turn opposite of the way the hands of a clock turn. It is a turn to the left.
This diagram shows Figure A turned counterclockwise to make Figure B.
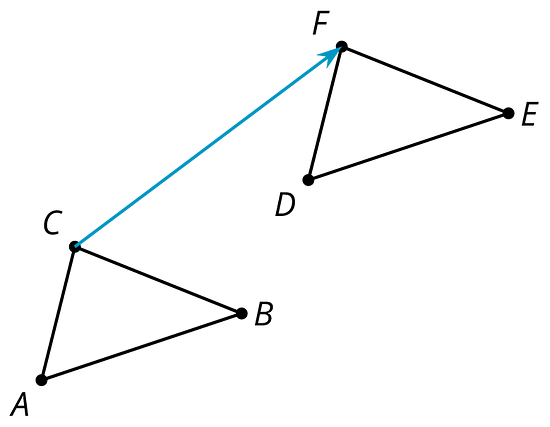
An image is the result of translations, rotations, and reflections on an object. Every part of the original object moves in the same way to match up with a part of the image.
In this diagram, triangle has been translated up and to the right to make triangle . Triangle is the image of the original triangle .
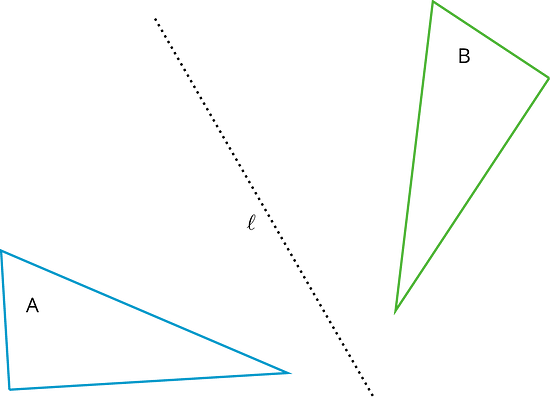
A reflection across a line moves every point on a figure to a point directly on the opposite side of the line. The new point is the same distance from the line as it was in the original figure.
This diagram shows a reflection of A over line that makes the mirror image B.
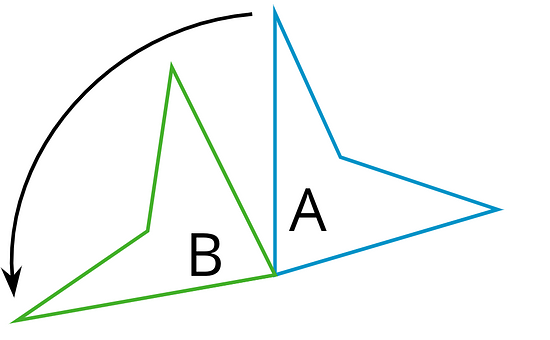
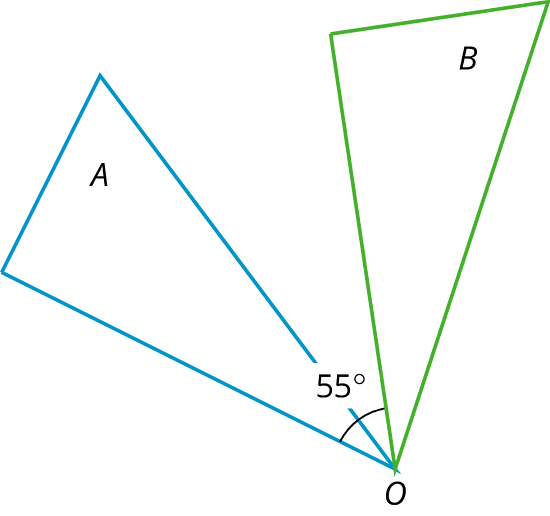
A rotation moves every point on a figure around a center by a given angle in a specific direction.
This diagram shows Triangle A rotated around center by 55 degrees clockwise to get Triangle B.
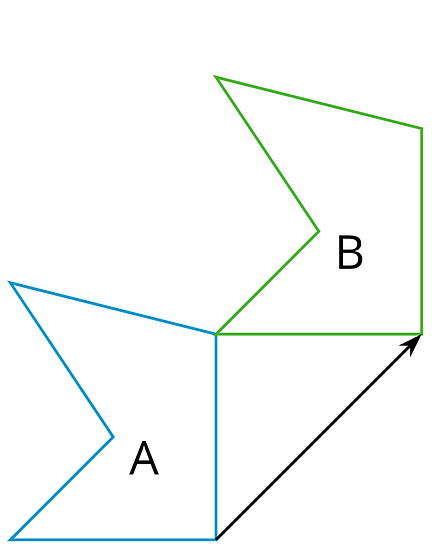
A translation moves every point in a figure a given distance in a given direction.
This diagram shows a translation of Figure A to Figure B using the direction and distance given by the arrow.
Lesson 2 Practice Problems
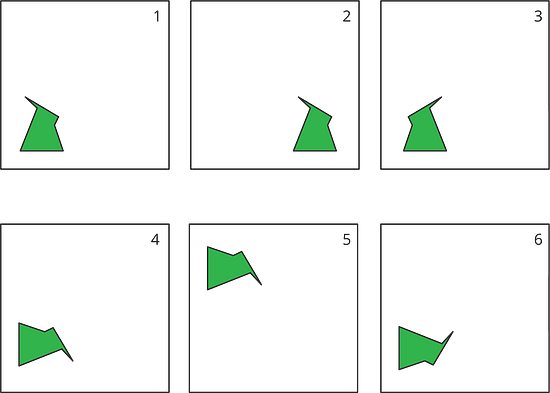
Each of the six cards shows a shape.

- Which pair of cards shows a shape and its image after a rotation?
- Which pair of cards shows a shape and its image after a reflection?
The five frames show a shape's different positions.
 Describe how the shape moves to get from its position in each frame to the next.
Describe how the shape moves to get from its position in each frame to the next.The rectangle seen in Frame 1 is rotated to a new position, seen in Frame 2.
Select all the ways the rectangle could have been rotated to get from Frame 1 to Frame 2.
- 40 degrees clockwise
- 40 degrees counterclockwise
- 90 degrees clockwise
- 90 degrees counterclockwise
- 140 degrees clockwise
- 140 degrees counterclockwise