Open Up Resources Logo

Lesson 5Coordinate Moves

Let’s transform some figures and see what happens to the coordinates of points.

Learning Targets:

  • I can apply transformations to points on a grid if I know their coordinates.

5.1 Translating Coordinates

Select all of the translations that take Triangle T to Triangle U. There may be more than one correct answer.

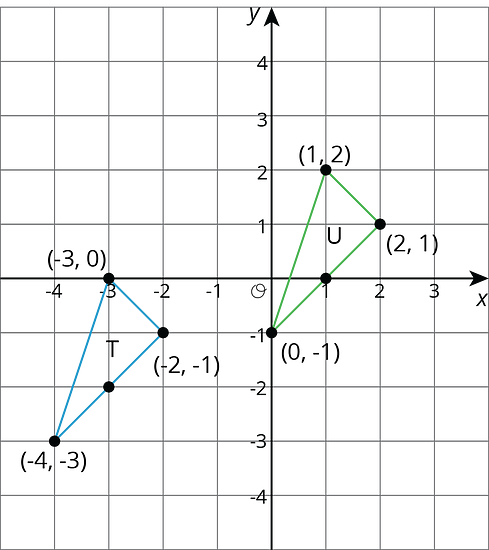
Two triangles on a coordinate grid. Triangle U has vertices (1, 2), (2,1), (0, -1). Triangle T has vertices (-3,0), (-2,-1), (-4, -3)
  1. Translate (\text-3,0) to (1,2) .
  2. Translate (2,1) to (\text-2,\text-1) .
  3. Translate (\text-4,\text-3) to (0,\text-1) .
  4. Translate (1,2) to (2,1) .

5.2 Reflecting Points on the Coordinate Plane

  1. Five points are plotted on the coordinate plane.

    open applet in presentation mode

    1. Using the Pen tool or the Text tool, label each with its coordinates.

    2. Using the x -axis as the line of reflection, plot the image of each point.

    3. Label the image of each point using a letter. For example, the image of point A should be labeled A’ .

    4. Label each with its coordinates.

  2. If the point (13,10) were reflected using the x -axis as the line of reflection, what would be coordinates of the image? What about (13, \text-20) ? (13, 570) ? Explain how you know.

  3. The point R has coordinates (3,2) .

    1. Without graphing, predict the coordinates of the image of point R if point R were reflected using the y -axis as the line of reflection.

    2. Check your answer by finding the image of R on the graph.

      Point R is at a (3,2) on a graph.

    3. Label the image of point R as  R’ .

    4. What are the coordinates of R’ ?

  4. Suppose you reflect a point using the y -axis as line of reflection. How would you describe its image?

5.3 Transformations of a Segment

The applet has instructions for the first 3 questions built into it. Move the slider marked “question” when you are ready to answer the next one. Pause before using the applet to show the transformation described in each question to predict where the new coordinates will be.

Apply each of the following transformations to segment AB . Use the Pen tool to record the coordinates.

  1. Rotate segment AB 90 degrees counterclockwise around center B by moving the slider marked 0 degrees. The image of A is named C . What are the coordinates of C ?

  2. Rotate segment AB 90 degrees counterclockwise around center A by moving the slider marked 0 degrees. The image of B is named D . What are the coordinates of D ?

  3. Rotate segment AB 90 degrees clockwise around (0,0) by moving the slider marked 0 degrees. The image of A is named E and the image of B is named F . What are the coordinates of E and F ?

  4. Compare the two 90-degree counterclockwise rotations of segment AB . What is the same about the images of these rotations? What is different?  

Are you ready for more?

Suppose EF and GH are line segments of the same length.  Describe a sequence of transformations that moves EF  to GH .

Lesson 5 Summary

We can use coordinates to describe points and find patterns in the coordinates of transformed points.

We can describe a translation by expressing it as a sequence of horizontal and vertical translations.  For example, segment AB is translated right 3 and down 2.

A trapezoid is formed by points (-2,1), (1,2), (4,0), and (1,-1).

Reflecting a point across an axis changes the sign of one coordinate. For example, reflecting the point A whose coordinates are (2,\text-1) across the x -axis changes the sign of the y -coordinate, making its image the point A’ whose coordinates are (2,1) . Reflecting the point A across the y -axis changes the sign of the x -coordinate, making the image the point A’’ whose coordinates are (\text-2,\text-1) .

Points are at (2,1), (2,-1), and (-2,-1)

Reflections across other lines are more complex to describe.

We don’t have the tools yet to describe rotations in terms of coordinates in general. Here is an example of a 90^\circ rotation with center (0,0) in a counterclockwise direction.

A right angle is created between points (-3,2), (0,0), and (2,3).

Point A has coordinates (0,0) . Segment AB was rotated 90^\circ counterclockwise around A . Point B with coordinates (2,3) rotates to point B’ whose coordinates are (\text-3,2) .

Lesson 5 Practice Problems

    1. Here are some points.
      Three points labeled, A, B, and C, plotted on a coordinate grid with the origin labeled “O.” The x axis has the numbers negative 10 through 8 indicated. The y axis has the numbers negative 4 through 6 indicated. Point A is located at negative 6 comma 5. Point B is located at 3 comma 2. Point C is located at 0 comma negative 1.

      What are the coordinates of A , B , and C after a translation to the right by 4 units and up 1 unit? Plot these points on the grid, and label them A’ , B’ and C’ .

    2. Here are some points.
      Three points labeled , D, E, and F, are plotted on a coordinate grid with the origin labeled “O.” The x axis has the numbers negative 5 through 5 indicated. The y axis has the numbers negative 2 through 3 indicated. Point D is located at negative 3 comma 3. Point E is located at 5 comma 0. Point F is located at 2 comma negative 2.

      What are the coordinates of D , E , and F after a reflection over the y -axis? Plot these points on the grid, and label them D’ , E’ and F’ .

    3. Here are some points.
      Three points labeled, G, H, and I, are plotted on a coordinate grid with the origin labeled “O.” Thex axis has the numbers negative 5 through 5 indicated. The y axis has the numbers negative 3 through 5 indicated. Point G is located at negative 1 comma 3. Point H is located at negative 4 comma 0. Point I is located at 3 comma negative 2.

      What are the coordinates of G , H , and I after a rotation about (0,0) by 90 degrees clockwise? Plot these points on the grid, and label them G’ , H’ and I’ .

  2. Describe a sequence of transformations that takes trapezoid A to trapezoid B.

    Trapezoids A and B are shown

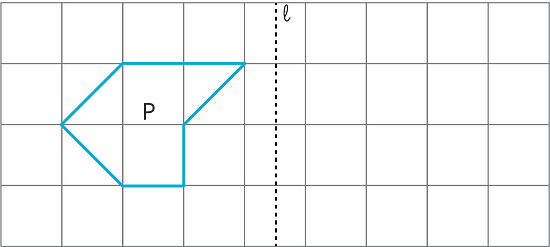
  3. Reflect polygon P using line \ell .

    Figure P is shown on a grid next to line l.