Lesson 3Dilations with no Grid
Let’s dilate figures not on grids.
Learning Targets:
- I can apply a dilation to a polygon using a ruler.
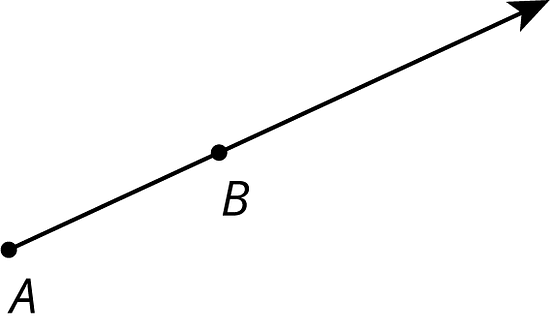
3.1 Points on a Ray
- Find and label a point on the ray whose distance from is twice the distance from to .
- Find and label a point on the ray whose distance from is half the distance from to .
3.2 Dilation Obstacle Course
-
Dilate using a scale factor of 5 and as the center of dilation. Which point is its image?
-
Using as the center of dilation, dilate so that its image is . What scale factor did you use?
-
Using as the center of dilation, dilate so that its image is . What scale factor did you use?
-
To dilate so that its image is , what point on the diagram can you use as a center?
-
Dilate using as the center and a scale factor of . Which point is its image?
-
Describe a dilation that uses a labeled point as its center and that would take to .
-
Using as the center of dilation, dilate so that its image is itself. What scale factor did you use?
3.3 Getting Perspective
Follow the directions to perform the dilations in the applet.
- Dilate using as the center and a scale factor of 4.
- Select the Dilate From Point tool.
- Click on the object to dilate, and then click on the center of dilation.
- When the dialog box opens, enter the scale factor. Fractions can be written with plain text, ex. 1/2.
- Click

- Use the Ray tool and the Distance tool to verify.
- Select the Dilate From Point tool.
- Dilate using as the center and a scale factor of .
- Draw a simple polygon. Choose a point not on the polygon to use as the center of dilation. Label it.
- Using your center point and a scale factor your teacher gives you, draw the image under the dilation of each vertex of the polygon, one at a time. Connect the dilated vertices to create the dilated polygon.
- Draw segments that connect each of the original vertices with its image. This will make your diagram look like a cool three-dimensional drawing of a box! If there's time, you can shade the sides of the box to make it look more realistic.
- Compare your drawing to other people’s drawings. What is the same and what is different? How do the choices you made affect the final drawing? Was your dilated polygon closer to your center point than to the original, or farther away? How is that determined?
Are you ready for more?
Here is line segment and its image under a dilation.
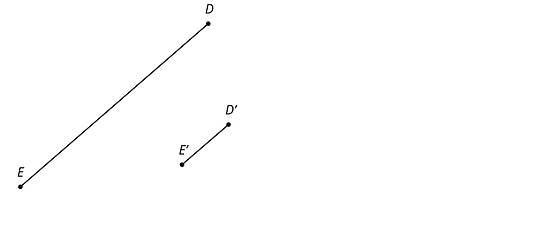
- Use a ruler to find and draw the center of dilation. Label it .
- What is the scale factor of the dilation?
Lesson 3 Summary
If is the center of dilation, how can we find which point is the dilation of with scale factor 2?

A dilation with scale factor less than 1 brings points closer. The point is the dilation of with center and scale factor .
Lesson 3 Practice Problems
Segment measures 3 cm. Point is the center of dilation. How long is the image of after a dilation with . . .
- Scale factor 5?
- Scale factor 3.7?
- Scale factor ?
- Scale factor ?
Here are points and . Plot the points for each dilation described.

- is the image of using as the center of dilation and a scale factor of 2.
- is the image of using as the center of dilation and a scale factor of 2.
- is the image of using as the center of dilation and a scale factor of .
- is the image of using as the center of dilation and a scale factor of .
- Make a perspective drawing. Include in your work the center of dilation, the shape you dilate, and the scale factor you use.
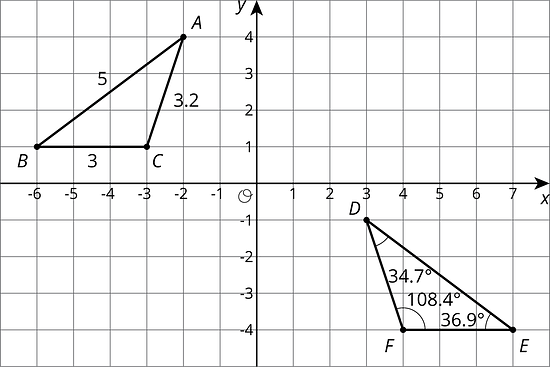
Triangle is a scaled copy of triangle . Side measures 12 cm and is the longest side of . Side measures 8 cm and is the longest side of .
- Triangle is a scaled copy of triangle with what scale factor?
- Triangle is a scaled copy of triangle with what scale factor?
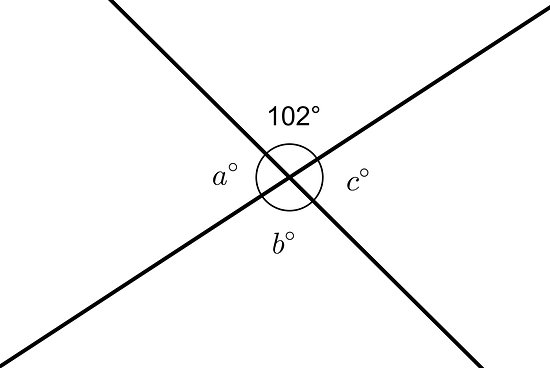
The diagram shows two intersecting lines.
Find the missing angle measures.
- Show that the two triangles are congruent.
- Find the side lengths of and the angle measures of .