Open Up Resources Logo

Lesson 7Similar Polygons

Let’s look at sides and angles of similar polygons.

Learning Targets:

  • I can use angle measures and side lengths to conclude that two polygons are not similar.
  • I know the relationship between angle measures and side lengths in similar polygons.

7.1 All, Some, None: Congruence and Similarity

Choose whether each of the statements is true in all cases, in some cases, or in no cases.

  1. If two figures are congruent, then they are similar.
  2. If two figures are similar, then they are congruent.
  3. If an angle is dilated with the center of dilation at its vertex, the angle measure may change.

7.2 Are They Similar?

  1. Let’s look at a square and a rhombus.
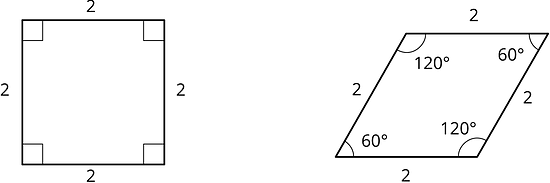
    There is a square with a side length of 2. Another parallelogram is shown with side lengths of 2 and two 60 degree and two 120 degree angles.

    Priya says, “These polygons are similar because their side lengths are all the same.” Clare says, “These polygons are not similar because the angles are different.” Do you agree with either Priya or Clare? Explain your reasoning.
  2. Now, let’s look at rectangles ABCD and EFGH .
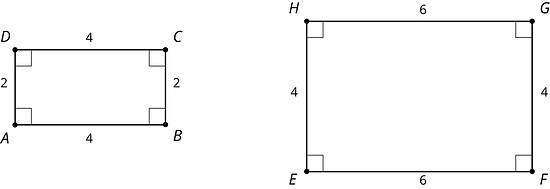
    Rectangle ABCD has a height of 2 and a width of 4. Rectangle EFGH has a height of 4 and a width of 6.

    Jada says, “These rectangles are similar because all of the side lengths differ by 2.” Lin says, “These rectangles are similar. I can dilate AD and BC using a scale factor of 2 and AB and CD using a scale factor of 1.5 to make the rectangles congruent. Then I can use a translation to line up the rectangles.” Do you agree with either Jada or Lin? Explain your reasoning.

Are you ready for more?

Two rectangles are shown with different shaded sectiosns.
Points A through H are translated to the right to create points A’ through H’ . All of the following are rectangles: GHBA , FCED , KH’C’J , and LJE’A’ . Which is greater, the area of blue rectangle DFCE or the total area of yellow rectangles KH’C’J and LJE’A’ ?

7.3 Find Someone Similar

Your teacher will give you a card. Find someone else in the room who has a card with a polygon that is similar but not congruent to yours. When you have found your partner, work with them to explain how you know that the two polygons are similar.

Are you ready for more?

On the left is an equilateral triangle where dashed lines have been added, showing how you can partition an equilateral triangle into smaller similar triangles.

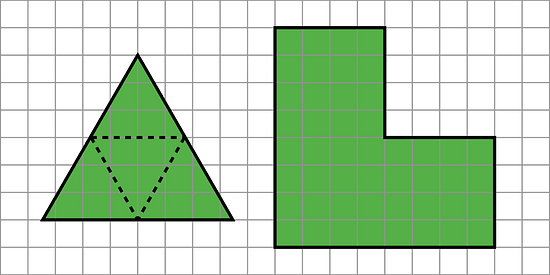
On the left is an equilateral triangle where dashed lines have been added, showing how you can partition an equilateral triangle into smaller similar triangles. Another L shaped figure is on the right.
Find a way to do this for the figure on the right, partitioning it into smaller figures which are each similar to that original shape. What’s the fewest number of pieces you can use? The most?

Lesson 7 Summary

When two polygons are similar:

  • Every angle and side in one polygon has a corresponding part in the other polygon.
  • All pairs of corresponding angles have the same measure.
  • Corresponding sides are related by a single scale factor. Each side length in one figure is multiplied by the scale factor to get the corresponding side length in the other figure.

Consider the two rectangles shown here. Are they similar?

Rectangle ABCD has a height of 3 and a width of 4. Rectangle EFGH has a height of 2 and a width of 3.

It looks like rectangles ABCD and EFGH could be similar, if you match the long edges and match the short edges. All the corresponding angles are congruent because they are all right angles. Calculating the scale factor between the sides is where we see that “looks like” isn’t enough to make them similar. To scale the long side AB to the long side EF , the scale factor must be \frac34 , because 4 \boldcdot \frac34=3 . But the scale factor to match AD to EH has to be \frac23 , because 3\boldcdot \frac23=2 . So, the rectangles are not similar because the scale factors for all the parts must be the same.

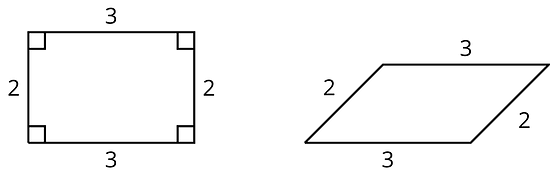
Here is an example that shows how sides can correspond (with a scale factor of 1), but the quadrilaterals are not similar because the angles don’t have the same measure:

Two quadrilaterals each wides opposite sides of 2 units and 3 units. The left quadrilateral has four right angles and the right quadrilateral has opposite angle that are equal.

Lesson 7 Practice Problems

  1. Triangle  DEF is a dilation of triangle ABC with scale factor 2. In triangle ABC , the largest angle measures 82^\circ . What is the largest angle measure in triangle DEF ?

    1. 41^\circ
    2. 82^\circ
    3. 123^\circ
    4. 164^\circ

  2. Draw two polygons that are similar but could be mistaken for not being similar. Explain why they are similar.

  3. Draw two polygons that are not similar but could be mistaken for being similar. Explain why they are not similar.

  4. These two triangles are similar. Find side lengths a and b . Note: the two figures are not drawn to scale.

    Two similar triangles are shown. One has lengths of 9 and 21. Side b is undetermines. The other triangle has lengths of 3 and 5. Side a is undetermined.

  5. Jada claims that B’C’D’ is a dilation of BCD using A as the center of dilation.

    What are some ways you can convince Jada that her claim is not true?

    Connecting line segments and points are shown
    1. Draw a horizontal line segment AB .
    2. Rotate segment AB 90^\circ counterclockwise around point A . Label any new points.
    3. Rotate segment AB 90^\circ clockwise around point B . Label any new points.
    4. Describe a transformation on segment AB you could use to finish building a square.