Lesson 12Solutions to Linear Equations
Let’s think about what it means to be a solution to a linear equation with two variables in it.
Learning Targets:
- I know that the graph of an equation is a visual representation of all the solutions to the equation.
- I understand what the solution to an equation in two variables is.
12.1 Estimate Area
Which figure has the largest shaded region?

12.2 Apples and Oranges
At the corner produce market, apples cost $1 each and oranges cost $2 each.
- Find the cost of:
- 6 apples and 3 oranges
- 4 apples and 4 oranges
- 5 apples and 4 oranges
- 8 apples and 2 oranges
-
Noah has $10 to spend at the produce market. Can he buy 7 apples and 2 oranges? Explain or show your reasoning.
-
What combinations of apples and oranges can Noah buy if he spends all of his $10?
-
Use two variables to write an equation that represents $10-combinations of apples and oranges. Be sure to say what each variable means.
-
What are 3 combinations of apples and oranges that make your equation true? What are three combinations of apples and oranges that make it false?
Are you ready for more?
- Graph the equation you wrote relating the number of apples and the number of oranges.
- What is the slope of the graph? What is the meaning of the slope in terms of the context?
- Suppose Noah has $20 to spend. Graph the equation describing this situation. What do you notice about the relationship between this graph and the earlier one?
12.3 Solutions and Everything Else
You have two numbers. If you double the first number and add it to the second number, the sum is 10.
-
Let represent the first number and let represent the second number. Write an equation showing the relationship between , , and 10.
-
Draw and label a set of - and -axes. Plot at least five points on this coordinate plane that make the statement and your equation true. What do you notice about the points you have plotted?
-
List ten points that do not make the statement true. Using a different color, plot each point in the same coordinate plane. What do you notice about these points compared to your first set of points?
Lesson 12 Summary
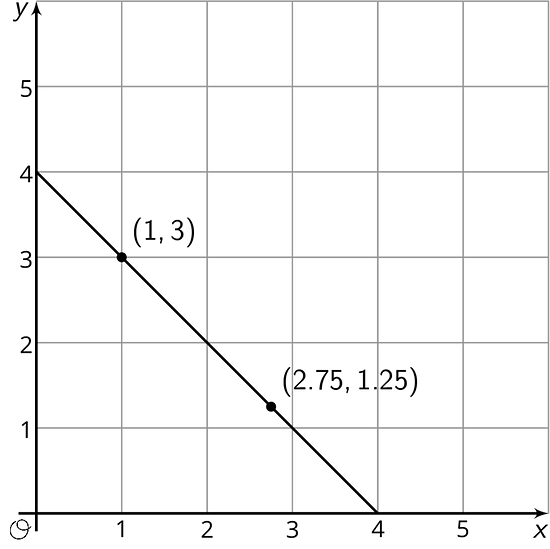
Think of all the rectangles whose perimeters are 8 units. If represents the width and represents the length, then expresses the relationship between the width and length for all such rectangles.
For example, the width and length could be 1 and 3, since or the width and length could be 2.75 and 1.25, since .
We could find many other possible pairs of width and length, , that make the equation true—that is, pairs that when substituted into the equation make the left side and the right side equal.
A solution to an equation with two variables is any pair of values that make the equation true.
We can think of the pairs of numbers that are solutions of an equation as points on the coordinate plane. Here is a line created by all the points that are solutions to . Every point on the line represents a rectangle whose perimeter is 8 units. All points not on the line are not solutions to .
Glossary Terms
A solution to an equation with two variables is a pair of values of the variables that make the equation true.
For example, one possible solution to the equation is . Substituting 6 for and 0 for makes this equation true because .
Lesson 12 Practice Problems
Select all of the ordered pairs that are solutions to the linear equation .
The graph shows a linear relationship between and .
represents the number of comic books Priya buys at the store, all at the same price, and represents the amount of money (in dollars) Priya has after buying the comic books.
- Find and interpret the - and -intercepts of this line.
- Find and interpret the slope of this line.
- Find an equation for this line.
- If Priya buys 3 comics, how much money will she have remaining?
Match each equation with its three solutions.
- , ,
- , ,
- , ,
- , ,
- , ,
A container of fuel dispenses fuel at the rate of 5 gallons per second. If represents the amount of fuel remaining in the container, and represents the number of seconds that have passed since the fuel started dispensing, then and satisfy a linear relationship.
In the coordinate plane, will the slope of the line representing that relationship have a positive, negative, or zero slope? Explain how you know.
A sandwich store charges a delivery fee to bring lunch to an office building. One office pays $33 for 4 turkey sandwiches. Another office pays $61 for 8 turkey sandwiches. How much does each turkey sandwich add to the cost of the delivery? Explain how you know.