Lesson 4Comparing Proportional Relationships
Let’s compare proportional relationships.
Learning Targets:
- I can compare proportional relationships represented in different ways.
4.1 What's the Relationship?
The equation could represent a variety of different situations.
-
Write a description of a situation represented by this equation. Decide what quantities and represent in your situation.
-
Make a table and a graph that represent the situation.
4.2 Summer Jobs
-
Elena and Jada each make money by helping out their neighbors.
Elena babysits. Her earnings are given by the equation , where represents how many hours she works and represents how much money she earns.
Jada earns $7 per hour mowing her neighbors’ lawns.
- Who makes more money after working 12 hours? How much more do they make? Explain how you know.
- What is the rate of change for each situation and what does it mean?
- How long would it take each person to earn $150? Explain or show your reasoning.
-
Han and Clare have summer jobs stuffing envelopes for two different companies.
Han earns $15 for every 300 envelopes he finishes.
Clare’s earnings:
number of envelopes money in dollars 400 40 900 90 - Who would make more money after stuffing 1,500 envelopes? How much more money would they make? Explain how you know.
- What is the rate of change for each situation and what does it mean?
- Who gets paid more in their job? Explain or show your reasoning.
-
Tyler plans to start a lemonade stand and is trying out different recipes for lemonade. He wants to make sure the recipe doesn’t use too much lemonade mix (lemon juice and sugar) but still tastes good.
Recipe 1 is given by the equation where represents the cups of lemonade mix and represents the cups of water.
Recipe 2:
lemonade mix (cups) water (cups) 10 50 13 65 21 105 - If Tyler had 16 cups of lemonade mix, how many cups of water would he need for each recipe? Explain how you know.
- What is the rate of change for each situation and what does it mean?
- Tyler has a 5-gallon jug (which holds 80 cups) to use for his lemonade stand and 16 cups of lemonade mix. Which lemonade recipe should he use? Explain or show your reasoning.
Are you ready for more?
Han and Clare are still stuffing envelopes. Han can stuff 20 envelopes in a minute, and Clare can stuff 10 envelopes in a minute. They start working together on a pile of 1,000 envelopes.
- How long does it take them to finish the pile?
- Who earns more money?
Lesson 4 Summary
When two proportional relationships are represented in different ways, we compare them by finding a common piece of information. For example:
Clare’s earnings are represented by the equation , where is the amount of money she earns, in dollars, for working hours.
The table shows some information about Jada’s pay.
| time worked (hours) | earnings (dollars) |
|---|---|
| 7 | 92.75 |
| 4.5 | 59.63 |
| 37 | 490.25 |
Who is paid at a higher rate per hour? How much more does that person have after 20 hours?
In Clare’s equation we see that the constant of proportionality relating her earnings to time worked is 14.50. This means that she earns $14.50 per hour.
We can calculate Jada’s constant of proportionality by dividing a value in the earnings column by a value in the same row in the time worked column. Using the last row, the constant of proportionality for Jada is 13.25, since . An equation representing Jada’s earnings is . This means she earns $13.25 per hour.
So Clare is paid at a higher rate than Jada. Clare earns $1.25 more per hour than Jada, which means that after 20 hours of work, she has more than Jada.
Lesson 4 Practice Problems
A contractor must haul a large amount of dirt to a work site. She collected information from two hauling companies. EZ Excavation gives its prices in a table. Happy Hauling Service gives its prices in a graph.
dirt (cubic yards) cost (dollars) 8 196 20 490 26 637 - How much would each hauling company charge to haul 40 cubic yards of dirt? Explain or show your reasoning.
- Calculate the rate of change for each relationship. What do they mean for each company?
- If the contractor has 40 cubic yards of dirt to haul and a budget of $1000, which hauling company should she hire? Explain or show your reasoning.
Andre and Priya are tracking the number of steps they walk. Andre records that he can walk 6000 steps in 50 minutes. Priya writes the equation , where is the number of steps and is the number of minutes she walks, to describe her step rate. This week, Andre and Priya each walk for a total of 5 hours. Who walks more steps? How many more?
Find the coordinates of point in each diagram:
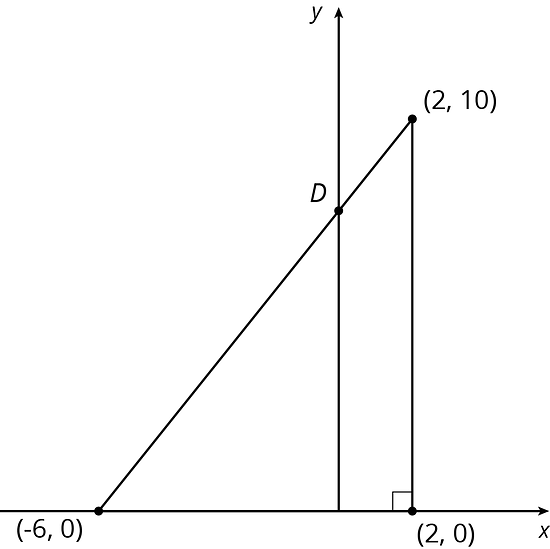
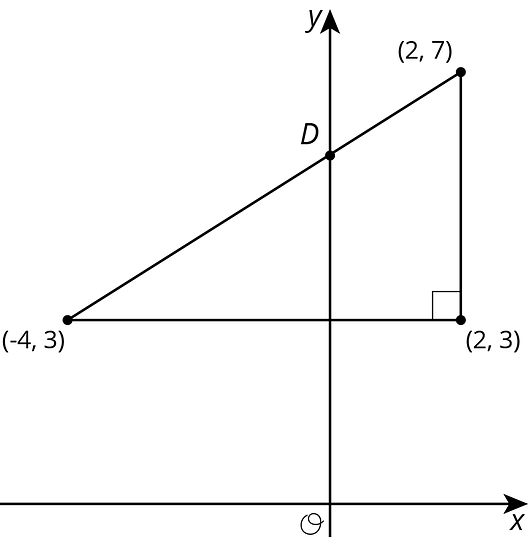
Select all the pairs of points so that the line between those points has slope .
- and
- and
- and
- and
- and