Lesson 13Solving Systems of Equations
Let’s solve systems of equations.
Learning Targets:
- I can graph a system of equations.
- I can solve systems of equations using algebra.
13.1 True or False: Two Lines
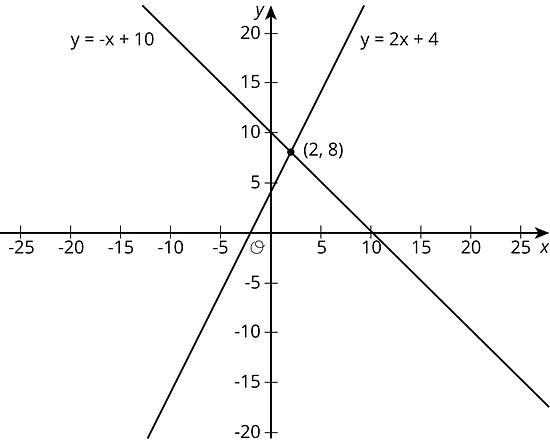
Use the lines to decide whether each statement is true or false. Be prepared to explain your reasoning using the lines.
- A solution to is 2.
- A solution to is 8.
- A solution to is 8.
- A solution to is 2.
- There are no values of and that make and true at the same time.
13.2 Matching Graphs to Systems
Here are three systems of equations graphed on a coordinate plane:
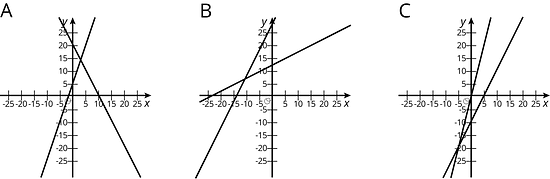
- Match each figure to one of the systems of equations shown here.
-
- Find the solution to each system and then check that your solution is reasonable on the graph.
- Notice that the sliders set the values of the coefficient and the constant term in each equation.
- Change the sliders to the values of the coefficient and the constant term in the next pair of equations.
- Click on the spot where the lines intersect and a labeled point should appear.
13.3 Different Types of Systems
Your teacher will give you a page with 6 systems of equations.
-
Graph each system of equations by typing each pair of the equations in the applet, one at a time.
- Describe what the graph of a system of equations looks like when it has . . .
- 1 solution
- 0 solutions
- infinitely many solutions
Use the applet to confirm your answer to question 2.
Are you ready for more?
The graphs of the equations and intersect at . Find and . Show or explain your reasoning.
Lesson 13 Summary
Sometimes it is easier to solve a system of equations without having to graph the equations and look for an intersection point. In general, whenever we are solving a system of equations written as
we know that we are looking for a pair of values that makes both equations true. In particular, we know that the value for will be the same in both equations. That means that
For example, look at this system of equations:
Since the value of the solution is the same in both equations, then we know
We can solve this equation for :
But this is only half of what we are looking for: we know the value for , but we need the corresponding value for . Since both equations have the same value, we can use either equation to find the -value:
Or
In both cases, we find that . So the solution to the system is . We can verify this by graphing both equations in the coordinate plane.
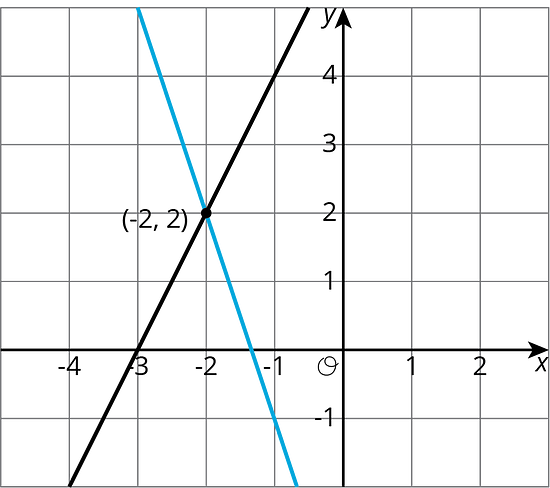
In general, a system of linear equations can have:
- No solutions. In this case, the lines that correspond to each equation never intersect.
- Exactly one solution. The lines that correspond to each equation intersect in exactly one point.
- An infinite number of solutions. The graphs of the two equations are the same line!
Lesson 13 Practice Problems
-
Write equations for the lines shown.
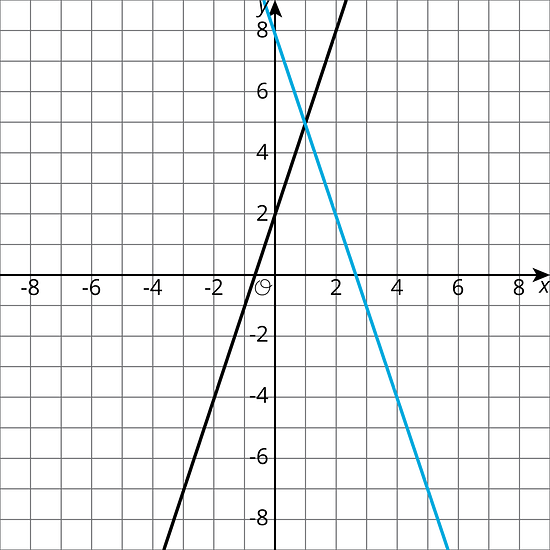
-
Describe how to find the solution to the corresponding system by looking at the graph.
-
Describe how to find the solution to the corresponding system by using the equations.
-
The solution to a system of equations is . Choose two equations that might make up the system.
-
Solve the system of equations:
Solve the system of equations:
Here is an equation:
- Solve the equation by using the distributive property first.
- Solve the equation without using the distributive property.
- Check your solution.