Lesson 8How Many Solutions?
Let’s solve equations with different numbers of solutions.
Learning Targets:
- I can solve equations with different numbers of solutions.
8.1 Matching Solutions
Consider the unfinished equation . Match the following expressions with the number of solutions the equation would have with that expression on the right hand side.
- One solution?
- No solutions?
- All solutions?
8.2 Thinking About Solutions Some More
Your teacher will give you some cards.
- With your partner, solve each equation.
- Then, sort them into categories.
- Describe the defining characteristics of those categories and be prepared to share your reasoning with the class.
8.3 Make Use of Structure
For each equation, determine whether it has no solutions, exactly one solution, or is true for all values of (and has infinitely many solutions). If an equation has one solution, solve to find the value of that makes the statement true.
-
-
-
- -
- -
- -
-
-
- What do you notice about equations with one solution? How is this different from equations with no solutions and equations that are true for every ?
Are you ready for more?
Consecutive numbers follow one right after the other. An example of three consecutive numbers is 17, 18, and 19. Another example is -100, -99, -98.
- Choose any set of three consecutive numbers. Find their average. What do you notice?
- Find the average of another set of three consecutive numbers. What do you notice?
- Explain why the thing you noticed must always work, or find a counterexample.
Lesson 8 Summary
Sometimes it's possible to look at the structure of an equation and tell if it has infinitely many solutions or no solutions. For example, look at
Using the distributive property on the left and right sides, we get
From here, collecting like terms gives us
Since the left and right sides of the equation are the same, we know that this equation is true for any value of without doing any more moves!
Similarly, we can sometimes use structure to tell if an equation has no solutions. For example, look at
If we think about each move as we go, we can stop when we realize there is no solution:
The last move makes it clear that the constant terms on each side, 5 and , are not the same. Since adding 5 to an amount is always less than adding to that same amount, we know there are no solutions.
Doing moves to keep an equation balanced is a powerful part of solving equations, but thinking about what the structure of an equation tells us about the solutions is just as important.
Glossary Terms
In an expression like , the number 2 is called the constant term because it doesn’t change when changes.
In the expression , 9 is the constant term.
In the expression , -8 is the constant term.
In the expression , 12 is the constant term.
Lesson 8 Practice Problems
Lin was looking at the equation . She said, “I can tell right away there are no solutions, because on the left side, you will have and a bunch of constants, but you have just on the right side.” Do you agree with Lin? Explain your reasoning.
Han was looking at the equation . He said, “I can tell right away there are no solutions, because on the left side, you will have and a bunch of constants, but you have just on the right side.” Do you agree with Han? Explain your reasoning.
Decide whether each equation is true for all, one, or no values of .
Solve each of these equations. Explain or show your reasoning.
-
The points and are each on the graph of a linear equation. Is also on the graph of this linear equation? Explain your reasoning.
In the picture triangle is an image of triangle after a rotation. The center of rotation is .
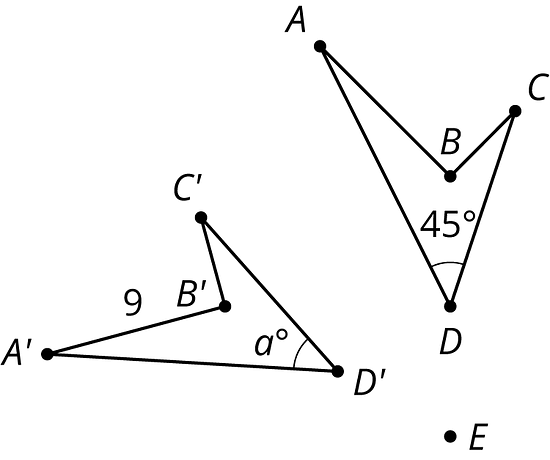
- What is the length of side ? Explain how you know.
- What is the measure of angle ? Explain how you know.