Lesson 21Cylinders, Cones, and Spheres
Let’s find the volume of shapes.
Learning Targets:
- I can find the radius of a sphere if I know its volume.
- I can solve mathematical and real-world problems about the volume of cylinders, cones, and spheres.
21.1 Sphere Arguments
Four students each calculated the volume of a sphere with a radius of 9 centimeters and they got four different answers.
- Han thinks it is 108 cubic centimeters.
- Jada got cubic centimeters.
- Tyler calculated 972 cubic centimeters.
- Mai says it is cubic centimeters.
Do you agree with any of them? Explain your reasoning.
21.2 Sphere’s Radius
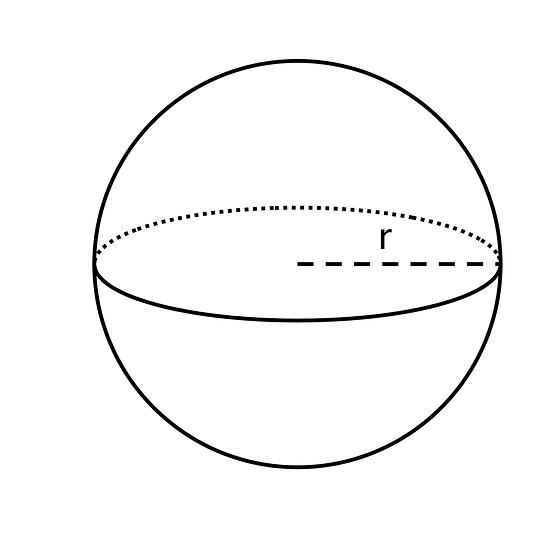
The volume of this sphere with radius is . This statement is true:
21.3 Info Gap: Unknown Dimensions
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
- Silently read your card and think about what information you need to answer the question.
- Ask your partner for the specific information that you need.
- Explain to your partner how you are using the information to solve the problem.
- Solve the problem and explain your reasoning to your partner.
If your teacher gives you the data card:
- Silently read the information on your card.
- Ask your partner “What specific information do you need?” and wait for your partner to ask for information. Only give information that is on your card. (Do not figure out anything for your partner!)
- Before telling your partner the information, ask “Why do you need that information?”
- After your partner solves the problem, ask them to explain their reasoning and listen to their explanation.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
21.4 The Right Fit
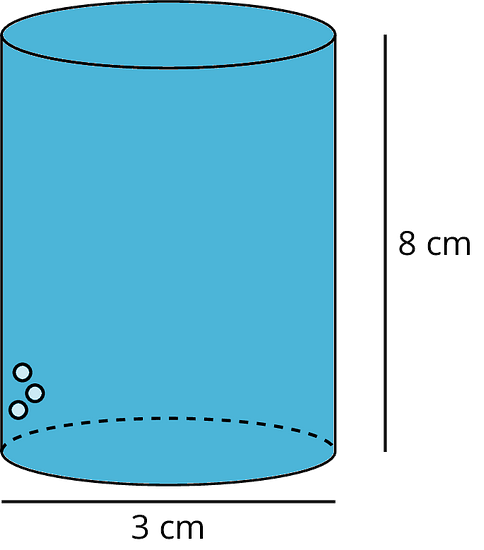
A cylinder with diameter 3 centimeters and height 8 centimeters is filled with water. Decide which figures described here, if any, could hold all of the water from the cylinder. Explain your reasoning.
- Cone with a height of 8 centimeters and a radius of 3 centimeters.
- Cylinder with a diameter of 6 centimeters and height of 2 centimeters.
- Rectangular prism with a length of 3 centimeters, width of 4 centimeters, and height of 8 centimeters.
- Sphere with a radius of 2 centimeters.
Are you ready for more?
A thirsty crow wants to raise the level of water in a cylindrical container so that it can reach the water with its beak.
- The container has diameter of 2 inches and a height of 9 inches.
- The water level is currently at 6 inches.
- The crow can reach the water if it is 1 inch from the top of the container.
Lesson 21 Summary
The formula
gives the volume of a sphere with radius . We can use the formula to find the volume of a sphere with a known radius. For example, if the radius of a sphere is 6 units, then the volume would be
or approximately cubic units. We can also use the formula to find the radius of a sphere if we only know its volume. For example, if we know the volume of a sphere is cubic units but we don't know the radius, then this equation is true:
That means that , so the radius has to be 3 units in order for both sides of the equation to have the same value.
Many common objects, from water bottles to buildings to balloons, are similar in shape to rectangular prisms, cylinders, cones, and spheres—or even combinations of these shapes! Using the volume formulas for these shapes allows us to compare the volume of different types of objects, sometimes with surprising results.
For example, a cube-shaped box with side length 3 centimeters holds less than a sphere with radius 2 centimeters because the volume of the cube is 27 cubic centimeters (), and the volume of the sphere is around 33.51 cubic centimeters ().
Lesson 21 Practice Problems
A scoop of ice cream has a 1.5 inch radius. How tall should the ice cream cone of the same radius be in order to contain all of the ice cream inside the cone?
Calculate the volume of the following shapes with the given information. For the first three questions, give each answer both in terms of and by using to approximate . Make sure to include units.
-
Sphere with a diameter of 6 inches
-
Cylinder with a height of 6 inches and a diameter of 6 inches
-
Cone with a height of 6 inches and a radius of 3 inches
-
How are these three volumes related?
-
A coin-operated bouncy ball dispenser has a large glass sphere that holds many spherical balls. The large glass sphere has a radius of 9 inches. Each bouncy ball has radius of 1 inch and sits inside the dispenser.
If there are 243 bouncy balls in the large glass sphere, what proportion of the large glass sphere’s volume is taken up by bouncy balls? Explain how you know.
A farmer has a water tank for cows in the shape of a cylinder with radius of 7 ft and a height of 3 ft. The tank comes equipped with a sensor to alert the farmer to fill it up when the water falls to 20% capacity. What is the volume of the tank be when the sensor turns on?