Lesson 3Equations for Functions
Let’s find outputs from equations.
Learning Targets:
- I can find the output of a function when I know the input.
- I can name the independent and dependent variables for a given function and represent the function with an equation.
3.1 A Square’s Area
Fill in the table of input-output pairs for the given rule. Write an algebraic expression for the rule in the box in the diagram.
| input | output |
|---|---|
| 8 | |
| 2.2 | |
3.2 Diagrams, Equations, and Descriptions
Record your answers to these questions in the table provided:
- Match each of these descriptions with a diagram:
- the circumference, , of a circle with radius,
- the distance in miles, , that you would travel in hours if you drive at 60 miles per hour
- the output when you triple the input and subtract 4
- the volume of a cube, , given its edge length,
- Write an equation for each description that expresses the output as a function of the input.
- Find the output when the input is 5 for each equation.
- Name the independent and dependent variables of each equation.
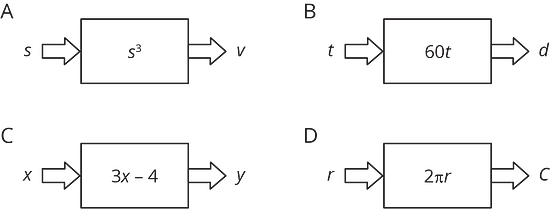
| description | a | b | c | d |
|---|---|---|---|---|
| diagram | ||||
| equation | ||||
| input = 5 output = ? |
||||
| independent variable |
||||
| dependent variable |
Are you ready for more?
Choose a 3-digit number as an input and apply the following rule to it, one step at a time:
- Multiply your number by 7.
- Add one to the result.
- Multiply the result by 11.
- Subtract 5 from the result.
- Multiply the result by 13
- Subtract 78 from the result to get the output.
Can you describe a simpler way to describe this rule? Why does this work?
3.3 Dimes and Quarters
Jada had some dimes and quarters that had a total value of $12.50. The relationship between the number of dimes, , and the number of quarters, , can be expressed by the equation .
- If Jada has 4 quarters, how many dimes does she have?
- If Jada has 10 quarters, how many dimes does she have?
- Is the number of dimes a function of the number of quarters? If yes, write a rule (that starts with ...) that you can use to determine the output, , from a given input, . If no, explain why not.
- If Jada has 25 dimes, how many quarters does she have?
- If Jada has 30 dimes, how many quarters does she have?
- Is the number of quarters a function of the number of dimes? If yes, write a rule (that starts with ...) that you can use to determine the output, , from a given input, . If no, explain why not.
Lesson 3 Summary
We can sometimes represent functions with equations. For example, the area, , of a circle is a function of the radius, , and we can express this with an equation:
We can also draw a diagram to represent this function:

In this case, we think of the radius, , as the input, and the area of the circle, , as the output. For example, if the input is a radius of 10 cm, then the output is an area of cm2, or about 314 square cm. Because this is a function, we can find the area, , for any given radius, .
Since it is the input, we say that is the independent variable and, as the output, is the dependent variable.
Sometimes when we have an equation we get to choose which variable is the independent variable. For example, if we know that
then we can think of as a function of and write
or we can think of as a function of and write
Glossary Terms
A dependent variable represents the output of a function.
We need to buy 20 pieces of fruit and decide to buy apples and bananas. If we select the number of apples first, the equation shows the number of bananas we can buy. The number of bananas is the dependent variable because it depends on the number of apples.
An independent variable is an amount that is used to calculate another amount. An independent variable represents the input of a function.
We need to buy 20 pieces of fruit and decide to buy some apples and bananas. If we select the number of apples first, the equation shows the number of bananas we can buy. The number of apples is the independent variable because we can choose any number for it.
Lesson 3 Practice Problems
Here is an equation that represents a function: .
Select all the different equations that describe the same function:
-
- Graph a system of linear equations with no solutions.
- Write an equation for each line you graph.
Brown rice costs $2 per pound, and beans cost $1.60 per pound. Lin has $10 to spend on these items to make a large meal of beans and rice for a potluck dinner. Let be the number of pounds of beans Lin buys and be the number of pounds of rice she buys when she spends all her money on this meal.
- Write an equation relating the two variables.
- Rearrange the equation so is the independent variable.
- Rearrange the equation so is the independent variable.
Solve each equation and check your answer.