Lesson 5More Graphs of Functions
Let’s interpret graphs of functions.
Learning Targets:
- I can explain the story told by the graph of a function.
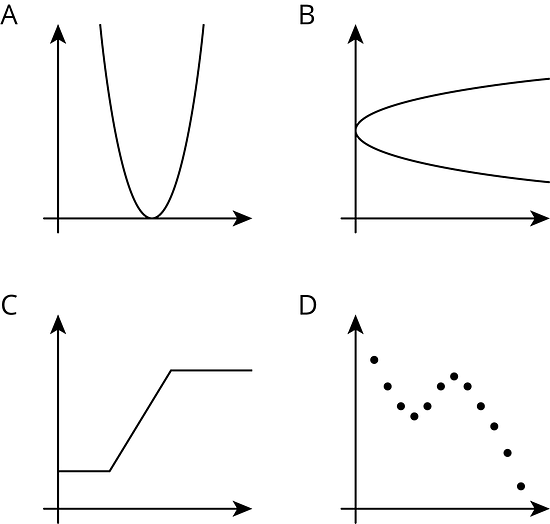
5.1 Which One Doesn’t Belong: Graphs
Which graph doesn’t belong?
5.2 Time and Temperature
The graph shows the temperature between noon and midnight in one day in a certain city.
- Was it warmer at 3:00 p.m. or 9:00 p.m.?
- Approximately when was the temperature highest?
- Find another time that the temperature was the same as it was at 4:00 p.m.
- Did the temperature change more between 1:00 p.m. and 3:00 p.m. or between 3:00 p.m. and 5:00 p.m.?
- Does this graph show that temperature is a function of time, or time is a function of temperature?
- When the input for the function is 8, what is the output? What does that tell you about the time and temperature?
5.3 Garbage
- The graph shows the amount of garbage produced in the US each year between 1991 and 2013.
- Did the amount of garbage increase or decrease between 1999 and 2000?
- Did the amount of garbage increase or decrease between 2005 and 2009?

“Garbage dump” by PublicDomainPictures via Pixabay. Public Domain. - Between 1991 and 1995, the garbage increased for three years, and then it decreased in the fourth year. Describe how the amount of garbage changed in the years between 1995 and 2000.
- The graph shows the percentage of garbage that was recycled between 1991 and 2013.
- When was it increasing?
- When was it decreasing?
- Tell the story of the change in the percentage of garbage recycled in the US over this time period.
Are you ready for more?
Refer to the graph in the first part of the activity.
- Find a year where the amount of garbage produced increased from the previous year, but not by as much it increased the following year.
- Find a year where the amount of garbage produced increased from the previous year, and then increased by a smaller amount the following year.
- Find a year where the amount of garbage produced decreased from the previous year, but not by as much it decreased the following year.
-
Find a year where the amount of garbage produced decreased from the previous year, and then decreased by a smaller amount the following year.
Lesson 5 Summary
Here is a graph showing the temperature in a town as a function of time after 8:00 p.m.
The graph of a function tells us what is happening in the context the function represents. In this example, the temperature starts out at F at 8:00 p.m. It decreases during the night, reaching its lowest point at 8 hours after 8:00 p.m., or 4:00 a.m. Then it starts to increase again.
Lesson 5 Practice Problems
Match each diagram to the function described, then label the axes appropriately
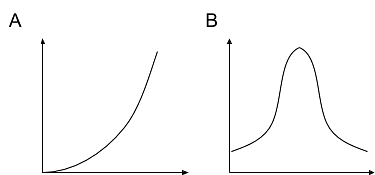
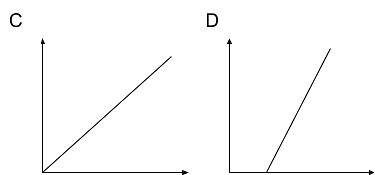
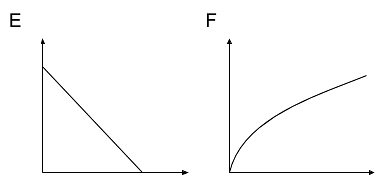
- The function inputs the age of an oak tree and outputs a prediction of the height of the tree .
- The function inputs the edge length of a cube and outputs the volume .
- The function inputs the distance traveled and predicts the amount of fuel left in the tank .
- The function inputs the height of a triangle with base 12 and outputs the area .
- The function inputs the time of day and predicts the temperature .
- The function inputs the time of day and predicts the number of cars washed at a student car wash .
The solution to a system of equations is . Choose two equations that might make up the system.
A car is traveling on a small highway and is either going 55 miles per hour or 35 miles per hour, depending on the speed limits, until it reaches its destination 200 miles away. Letting represent the amount of time in hours that the car is going 55 miles per hour, and being the time in hours that the car is going 35 miles per hour, an equation describing the relationship is:
- If the car spends 2.5 hours going 35 miles per hour on the trip, how long does it spend going 55 miles per hour?
- If the car spends 3 hours going 55 miles per hour on the trip, how long does it spend going 35 miles per hour?
- If the car spends no time going 35 miles per hour, how long would the trip take? Explain your reasoning.
The graph represents an object that is shot upwards from a tower and then falls to the ground. The independent variable is time in seconds and the dependent variable is the object’s height above the ground in meters.
- How tall is the tower from which the object was shot?
- When did the object hit the ground?
- Estimate the greatest height the object reached and the time it took to reach that height. Indicate this situation on the graph.