Lesson 2Side Lengths and Areas
Let’s investigate some more squares.
Learning Targets:
- I can explain what a square root is.
- I understand the meaning of expressions like and .
- If I know the area of a square, I can express its side length using square root notation.
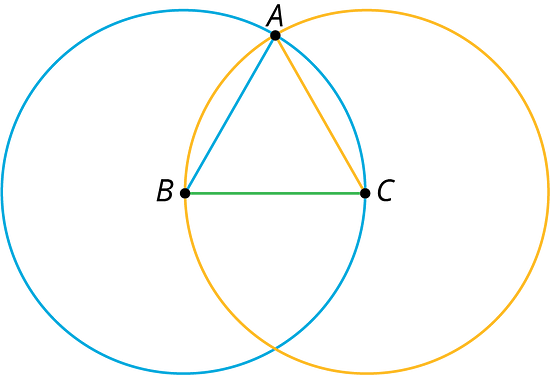
2.1 Notice and Wonder: Intersecting Circles
What do you notice? What do you wonder?
2.2 One Square
-
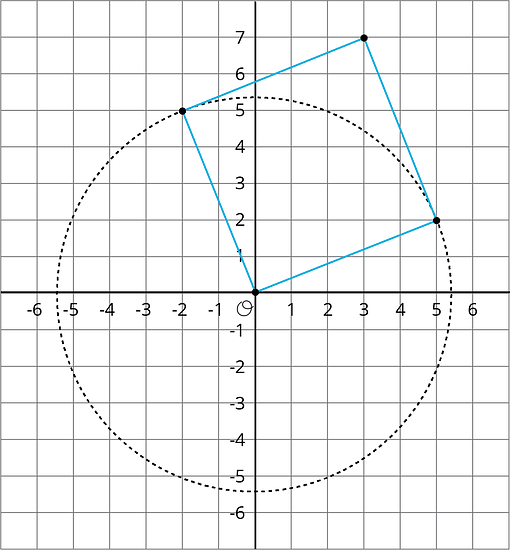
Use the circle to estimate the area of the square shown here:

-
Use the grid to check your answer to the first problem.
Are you ready for more?
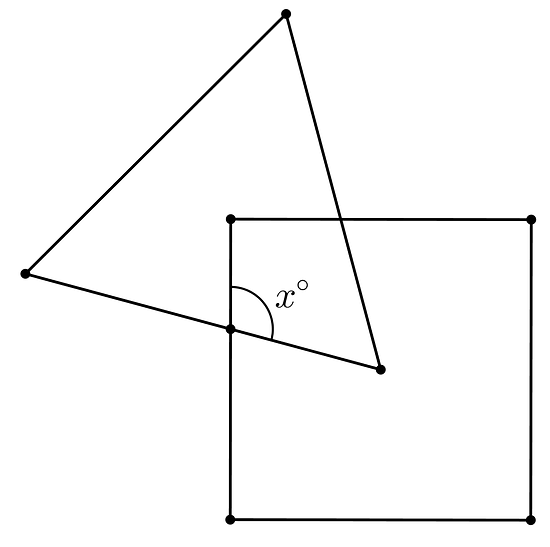
One vertex of the equilateral triangle is in the center of the square, and one vertex of the square is in the center of the equilateral triangle. What is ?
2.3 The Sides and Areas of Tilted Squares
-
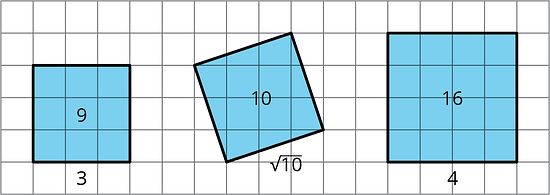
Find the area of each square and estimate the side lengths using your geometry toolkit. Then write the exact lengths for the sides of each square.

- Complete the tables with the missing side lengths and areas.
side length, 0.5 1.5 2.5 3.5 area, 1 4 9 16 side length, 4.5 5.5 6.5 7.5 area, 25 36 49 64 -
Plot the points, , on the coordinate plane shown here.
-
Use this graph to estimate the side lengths of the squares in the first question. How do your estimates from the graph compare to the estimates you made initially using your geometry toolkit?
-
Use the graph to approximate .
Lesson 2 Summary
We saw earlier that the area of square ABCD is 73 units2.

What is the side length? The area is between and , so the side length must be between 8 units and 9 units. We can also use tracing paper to trace a side length and compare it to the grid, which also shows the side length is between 8 units and 9 units. But we want to be able to talk about its exact length. In order to write “the side length of a square whose area is 73 square units,” we use the square root symbol. “The square root of 73” is written , and it means “the length of a side of a square whose area is 73 square units.”
We say the side length of a square with area 73 units2 is units. This means that
All of these statements are also true:
because
because
units is the side length of a square whose area is 10 units2, and
Glossary Terms
The square root of a positive number n is the positive number whose square is . It is also the the side length of a square whose area is . We write the square root of as .
For example, the square root of 16, written as , is 4 because is 16. is also the side length of a square that has an area of 16.
Lesson 2 Practice Problems
A square has an area of 81 square feet. Select all the expressions that equal the side length of this square, in feet.
-
-
-
9
-
-
3
-
Write the exact value of the side length, in units, of a square whose area in square units is:
- 36
- 37
- 0.0001
- 0.11
Square A is smaller than Square B. Square B is smaller than Square C.
The three squares’ side lengths are , 4.2, and .
What is the side length of Square A? Square B? Square C? Explain how you know.Find the area of a square if its side length is:
- cm
- units
- inches
- 0.1 meters
- 3.5 cm
Here is a table showing the areas of the seven largest countries.
- How much more area is there in Russia than in Canada?
- The Asian countries on this list are Russia, China, and India. The American countries are Canada, the United States, and Brazil. Which has the greater total area: the three Asian countries, or the three American countries?
country area (in km2) Russia Canada China United States Brazil Australia India Select all the expressions that are equivalent to .