Lección 8Escribamos y grafiquemos desigualdades
Escribamos desigualdades.
Metas de aprendizaje:
- Puedo escribir una desigualdad para representar una situación.
- Puedo graficar desigualdades sobre la recta numérica.
8.1 Estimemos la estatura de la gente
-
Esta es una foto de un hombre.

- Menciona un número, en pies, que sea evidentemente demasiado grande para la estatura de este hombre.
- Menciona un número, en pies, que sea evidentemente demasiado pequeño para la estatura de este hombre.
- Haz una estimación de la estatura del hombre.
Haz una pausa para tener una discusión con toda la clase.
-
Esta es una foto del mismo hombre parado junto a un niño.

Si la estatura real del hombre es 5 pies con 10 pulgadas, ¿qué puedes decir sobre la estatura del niño en esta foto?
Prepárate para explicar tu razonamiento.
8.2 Historias sobre el 9
Arrastra los puntos vacíos rojos y verdes sobre los puntos azules, asociando cada historia, gráfica y descripción.
- Escribe tus resultados usando un número seguido de una letra en mayúscula y una letra en minúscula. Por ejemplo, 1Aa significaría que las respuestas "1", "A" y "a" representan todas la misma situación.
- Piensa cómo representarías cada conjunto de números como una desigualdad, háblalo con tu compañero y prepárate para discutir tus ideas con la clase.
-
Escribe tus decisiones de asociación definitivas de la siguiente forma:
- Un bote pesquero puede llevar menos de 9 personas. ¿A cuántas personas (x) puede llevar?
-
Descripción o lista:
- Recta numérica:
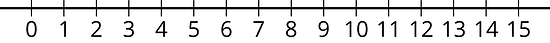
-
Desigualdad:
-
- Lin necesita más de 9 onzas de mantequilla para hacer galletas para su fiesta. ¿Cuántas onzas de mantequilla (x) serían suficientes?
-
Descripción o lista:
- Recta numérica:
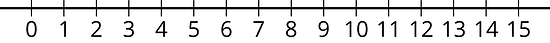
-
Desigualdad:
-
- Una maga hará sus trucos solo si hay por lo menos 9 personas en el público. ¿Para cuántas personas (x) hará sus trucos de magia?
-
Descripción o lista:
- Recta numérica:
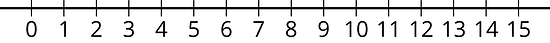
-
Desigualdad:
-
- Una báscula de alimentos puede medir pesos de hasta 9 kilogramos. ¿Qué pesos (x) puede medir la báscula?
-
Descripción o lista:
- Recta numérica:
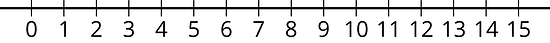
-
Desigualdad:
-
- Un bote pesquero puede llevar menos de 9 personas. ¿A cuántas personas (x) puede llevar?
8.3 ¿Qué tan alto y qué tan bajo puede estar?
Esta es una foto de una persona y un aro de baloncesto. Basándote en la foto, ¿cuáles piensas que serían unas estimaciones razonables para la altura máxima y mínima del aro de baloncesto?
-
Completa el primer espacio en cada oración con una estimación y el segundo espacio con "más alto" o "más bajo".

-
Yo estimo que la altura mínima del aro de baloncesto es _________ pies; esto significa que el aro no puede ser _____________ que esta altura.
-
Yo estimo que la altura máxima del aro de baloncesto es _________ pies; esto significa que el aro no puede ser _____________ que esta altura.
-
-
Escribe dos desigualdades: una para mostrar tu estimación de la altura mínima del aro de baloncesto y la otra para la altura máxima. Usa un símbolo de desigualdad y la variable para representar la altura desconocida.
-
Ubica cada estimación del valor mínimo o del máximo en la recta numérica.
Mínimo:
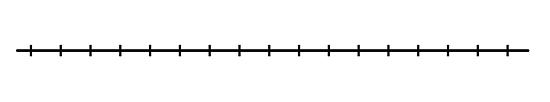
Máximo:
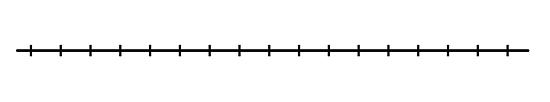
- Supongamos que un compañero estimó que el valor de es 19 pies. ¿Esta estimación cumple tu desigualdad de la altura máxima? ¿Cumple tu desigualdad de la altura mínima? Explica o muestra cómo lo sabes.
- Pídele a un compañero una estimación de . Anótala y verifica si cumple tus desigualdades de las alturas máxima y mínima.
¿Estás listo para más?
- Encuentra 3 números diferentes para , si . Ubica estos puntos en la recta numérica. Después, ubica tantas posibilidades para el valor de como puedas.

- Encuentra 3 números diferentes para , si . Ubica estos puntos en la recta numérica. Después, ubica tantas posibilidades para el valor de como puedas.

Resumen de la lección 8
Una desigualdad nos dice que un valor es menor que o mayor que otro valor.
Supongamos que sabemos que la temperatura es menor que , pero no sabemos cuánto es exactamente. Para representar lo que sabemos sobre la temperatura en , podemos escribir la desigualdad:
La temperatura también se puede graficar en una recta numérica. Cualquier punto a la izquierda de 3 es un valor posible para . El círculo vacío en 3 quiere decir que no puede ser igual a 3 porque la temperatura es menor que 3.

Este es otro ejemplo. Supongamos que un viajero joven debe tener por lo menos 16 años para viajar en avión sin un adulto que lo acompañe.
Si representa la edad del viajero, cualquier número mayor que 16 es un valor posible para y el mismo 16 también es un valor posible para . Podemos mostrar esto en una recta numérica dibujando un círculo relleno en 16 para mostrar que cumple el requerimiento (una persona de 16 años puede viajar sola). Desde ahí, dibujamos una línea que apunta hacia la derecha.

También podemos escribir una desigualdad y una ecuación para mostrar los valores posibles para :
Problemas de práctica de la lección 8
En una promoción de libros, todos los libros cuestan menos de $5.
- ¿Cuánto puede costar el libro más caro?
- Escribe una desigualdad para representar el precio de los libros en promoción.
- Dibuja una recta numérica para representar la desigualdad.
Kiran comenzó su tarea antes de las 7:00 p.m. y terminó su tarea después de las 8:00 p.m. Sea el número de horas que Kiran trabajó en su tarea.
Decide si cada expresión es definitivamente verdadera, definitivamente falsa o posiblemente verdadera. Explica tu razonamiento.
-
Considera un prisma rectangular de longitud 4 y altura .
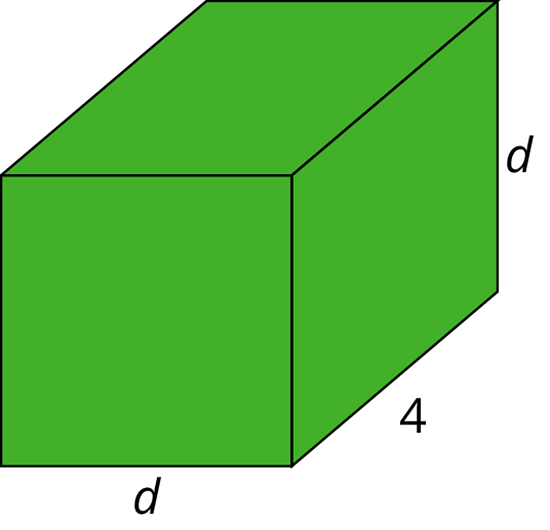
- Halla una expresión para el volumen del prisma en términos de .
- Calcula el volumen del prisma cuando , cuando y cuando .
Empareja los enunciados matemáticos con las afirmaciones escritas en español. Todos los enunciados son verdaderos.
- El número -15 está más lejos de 0 que el número -12 en la recta numérica.
- El número -12 está a una distancia de 12 unidades del 0 en la recta numérica.
- La distancia entre -12 y 0 en la recta numérica es mayor que -15.
- Los números 12 y -12 están a la misma distancia del 0 en la recta numérica.
- El número -15 es menor que el número -12.
- El número 12 es mayor que el número -12.
Estas son cinco sumas. Usa la propiedad distributiva para escribir cada suma como un producto con dos factores.