Lección 14Encontremos soluciones a desigualdades en un contexto
Resolvamos desigualdades más complicadas.
Metas de aprendizaje:
- Puedo describir las soluciones de una desigualdad resolviendo una ecuación relacionada y luego razonando sobre los valores que hacen verdadera la desigualdad.
- Puedo escribir una desigualdad para representar una situación.
14.1 Soluciones a ecuaciones y soluciones a desigualdades
-
Resuelve
-
Encuentra 2 soluciones para
-
Resuelve
-
Encuentra 2 soluciones para
14.2 Ganar dinero para comprar cosas de fútbol
-
Andre tiene un trabajo de verano vendiendo suscripciones a revistas. Gana $25 por semana más $3 por cada suscripción que vende. Andre espera ganar esta semana al menos suficiente dinero para comprar un nuevo par de zapatillas de fútbol.
- Escribe una expresión para la cantidad de dinero que gana Andre esta semana, en la que represente la cantidad de suscripciones a revistas que vende Andre esta semana.
- El par de zapatillas de fútbol menos costoso que Andre quiere cuestan $68. Escribe y resuelve una ecuación para averiguar cuántas suscripciones de revistas necesita vender Andre para comprar las zapatillas de fútbol.
- Si Andre vendiera 16 suscripciones a revistas esta semana, ¿alcanzaría su objetivo?. Explica tu razonamiento.
-
¿Qué otras cantidades de suscripciones a revistas podría haber vendido Andre y todavía alcanzar su objetivo?
- Escribe una desigualdad que exprese que Andre quiere ganar al menos $68.
-
Escribe una desigualdad para describir la cantidad de suscripciones que debe vender Andre para alcanzar su objetivo.
-
Diego ha presupuestado $35 de sus ganancias de trabajo de verano para comprar pantalonetas y medias para fútbol. Necesita 5 pares de medias y un par de pantalonetas. Las medias tienen diferentes costos en distintas tiendas. Las pantalonetas que quiere cuestan $19.95.
- Escribe una expresión para el costo total de las medias y las pantalonetas, en la que represente el costo de un par de medias.
- Escribe y resuelve una ecuación que diga que Diego gastó exactamente $35 en medias y pantalonetas.
- Realiza una lista de otros precios posibles para las medias que le permitan a Diego mantenerse dentro de su presupuesto.
-
Escribe una desigualdad para representar la cantidad que Diego puede gastar en un solo par de medias.
14.3 Barras de granola y ahorros
- Kiran tiene $100 ahorrados en una cuenta bancaria que no genera intereses. Le pidió a Clare que lo ayudara a averiguar cuánto podría retirar cada mes si necesita tener por lo menos $25 en la cuenta dentro de un año a partir de ahora.
- Clare escribió la desigualdad , donde representa la cantidad que Kiran retira cada mes. ¿Qué representa ?
- Encuentra algunos valores de que funcionarían para Kiran.
-
Podríamos expresar todos los valores que funcionarían utilizando . ¿Cuál deberíamos usar?
- Escribe la respuesta a la pregunta de Kiran usando notación matemática.
-
Un profesor quiere comprar 9 cajas de barras de granola para un viaje escolar. Cada caja generalmente cuesta $7, pero muchos supermercados tienen ofertas en barras de granola esta semana. Varias tiendas están vendiendo cajas de barras de granola con distintos descuentos.
- Si representa la cantidad en dólares del descuento, la cantidad que pagará el profesor se puede expresar como . En esta expresión, ¿qué representa la cantidad ?
- El profesor tiene $36 para gastar en las barras de granola. La ecuación representa una situación en la que él gasta todos los $36. Resuelve esta ecuación.
- ¿Qué significa la solución en esta situación?
- El profesor no tiene que gastar todos los $36. Escribe una desigualdad que relacione 36 y representando esta situación.
- La solución a esta desigualdad debe parecerse a . ¿Cuál crees que es? Explica tu razonamiento.
¿Estás listo para más?
Jada y Diego cocinaron una gran tanda de galletas.
- Seleccionaron de las galletas para darle a sus profesores.
- Luego descartaron una galleta quemada.
- Entregaron de las galletas restantes a un asilo de ancianos local.
- Luego, les dieron 3 galletas a algunos niños del barrio.
- Envolvieron de las galletas restantes para guardarlas a sus amigos.
Después de todo esto, les quedaban 15 galletas. ¿Cuántas galletas hornearon?
Resumen de la lección 14
Supongamos que Elena tiene $5 y vende bolígrafos a $1.50 cada uno. Su objetivo es ahorrar $20. Podríamos resolver la ecuación para encontrar la cantidad de bolígrafos, , que Elena necesita vender para ahorrar exactamente $20. Agregar -5 a ambos lados de la ecuación nos da , y luego dividir ambos lados entre da la solución bolígrafos.
¿Qué pasa si Elena quiere que le quede algo de dinero? La desigualdad nos dice que la cantidad de dinero que Elena necesita debe ser mayor a $20. La solución a la ecuación anterior nos ayudará a entender cuáles serán las soluciones a la desigualdad. Sabemos que si vende 10 bolígrafos, ganará $20. Ya que cada bolígrafo le da más dinero, necesita vender más de 10 bolígrafos para ganar más de $20. Entonces la solución a la desigualdad es .
Problemas de práctica de la lección 14
La solución de puede ser o . ¿Cuál solución es correcta? Explica cómo lo sabes.
El director de la banda escolar sabe por experiencia previa que si cobran dólares por una entrada al concierto, pueden esperar una asistencia de personas. El director usó este modelo para concluir que el precio de un boleto debe ser $8 o más para que asistan al menos 600 personas. ¿Estás de acuerdo con esta afirmación? ¿Por qué o por qué no?
¿Cuál desigualdad es verdadera cuando el valor de es -3?
Dibuja el conjunto solución de cada una de las siguientes desigualdades.
-
Escribe tres ecuaciones distintas que correspondan con el diagrama de cinta.

Un panadero quiere reducir la cantidad de azúcar en sus recetas de pasteles. Decide reducir la cantidad que usa en 1 pastel en taza. Después, él usa tazas de azúcar para hornear 6 pasteles.
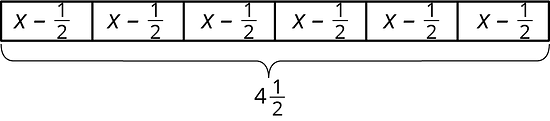
- Describe cómo el diagrama de cinta representa la historia.
- ¿Cuánto azúcar había originalmente en cada receta del pastel?
Hace un año, Clare medía 4 pies y 6 pulgadas de alto. Ahora, Clare mide 4 pies y 10 pulgadas de alto. ¿En qué porcentaje aumentó la estatura de Clare en el último año?