Lección 16Interpretemos desigualdades
Escribamos desigualdades.
Metas de aprendizaje:
- Puedo asociar una desigualdad a una situación que esta representa, resolverla y luego explicar que la significa la solución en la situación.
- Si tengo una situación y una desigualdad que la representa, puedo explicar que significan las partes de la desigualdad en la situación.
16.1 ¡Resolvamos desigualdades!
Para cada desigualdad, encuentra el valor o los valores de que la hacen verdadera.
16.2 Representemos las actividades de los clubes
Escoge la desigualdad que mejor pueda representar la situación dada. Explica tu razonamiento.
- El Club de Jardinería está plantando árboles frutales en el jardín de su escuela. Hay un árbol grande que necesita 5 libras de fertilizante. El resto son árboles recién plantados que necesitan libra de fertilizante cada uno.
- El Club de Química está experimentando con diferentes mezclas de agua con un cierto químico (poliacrilato de sodio) para hacer nieve artificial.
Para hacer cada mezcla, los estudiantes comienzan con cierta cantidad de agua y luego agregan de esa cantidad del químico y luego 9 gramos más del químico. El químico es costoso, por lo que no puede haber más de un cierto número de gramos del químico en cada una de las mezclas. - El Club de Senderismo está en una caminata por un acantilado. Comienzan a una elevación de 12 pies y descienden a una tasa de 3 pies por cada minuto.
- El Club de Ciencias está investigando puntos de ebullición. Aprenden que a altitudes altas, el agua hierve a temperaturas más bajas. Al nivel del mar, el agua hierve a . Con cada aumento de 500 pies en la elevación, el punto de ebullición del agua disminuye aproximadamente en .
16.3 Presentación de las actividades de los clubes
Tu profesor asignará a tu grupo una de las situaciones de la última tarea. Creen una presentación visual sobre la situación. En la presentación:
- Expliquen qué representan la variable y cada parte de la desigualdad
- Escriban una pregunta que pueda responderse con la solución de la desigualdad
- Muestren cómo resolvieron la desigualdad
- Expliquen qué significa la solución en términos de la situación
¿Estás listo para más?
es un conjunto de cuatro enteros consecutivos cuya suma es 18.
- ¿Cuántos conjuntos hay de tres enteros consecutivos cuya suma está entre 51 y 60? ¿Estás seguro de haberlos encontrado todos? Explica o muestra tu razonamiento.
- ¿Cuántos conjuntos hay de cuatro enteros consecutivos cuya suma está entre 59 y 82? ¿Estás seguro de haberlos encontrado todos? Explica o muestra tu razonamiento.
Resumen de la lección 16
Podemos representar y resolver muchos problemas del mundo real con desigualdades. Escribir las desigualdades es muy parecido a escribir ecuaciones para representar una situación. Las expresiones que componen las desigualdades son las mismas que hemos visto en lecciones anteriores para ecuaciones. Para las desigualdades, también debemos pensar cómo se comparan las expresiones entre sí, cuál es más grande y cuál es más pequeña. ¿Pueden también ser iguales?
Por ejemplo, una colecta de fondos para la escuela tiene un meta mínima de $500. El personal docente ha donado $100 y hay 12 clubes de estudiantes que participan con diferentes actividades. ¿Cuánto dinero debería recaudar cada club para alcanzar el objetivo de la colecta de fondos? Si es la cantidad de dinero que recauda cada club, entonces la solución de es la cantidad mínima que cada club debe recaudar para alcanzar el objetivo. Sin embargo, es más realista usar la desigualdad ya que mientras más dinero recaudemos, más exitosa será la colecta de fondos. Hay muchas soluciones porque hay muchas cantidades diferentes de dinero que los clubes podrían recaudar y que nos permitirían sobrepasar nuestra meta mínima de $500.
Problemas de práctica de la lección 16
Priya estudia la desigualdad y dice: "Resto un número de 12 y quiero un resultado mayor que 5. Eso significa que las soluciones deben ser valores de que sean más pequeños que algo".
¿Estás de acuerdo con Priya? Explica tu razonamiento e incluye soluciones a la desigualdad en tu explicación.
Cuando una tienda había vendido de las camisas que estaban exhibidas, esta sacó otras 30 del depósito. A la tienda le gusta tener por lo menos 150 exhibidas. El gerente escribió la desigualdad para describir la situación.
- Explica qué significa en la desigualdad.
- Resuelve la desigualdad.
- Explica qué significa una solución en el contexto de la situación.
Sabes que es un número menor que 4. Selecciona todas las desigualdades que deben ser verdaderas.
Este es un diagrama de colgador desbalanceado.
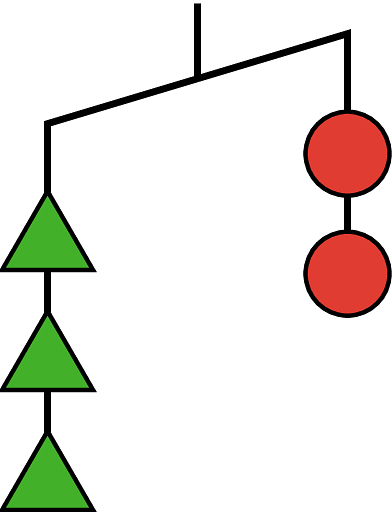
- Si supieras que cada círculo pesa 6 gramos, ¿qué te diría esto sobre el peso de cada triángulo?. Explica tu razonamiento.
- Si supieras que cada triángulo pesa 3 gramos, ¿qué te diría esto sobre el peso de cada círculo?. Explica tu razonamiento.
En una tienda de artículos para practicar patineta:
- El precio de una camiseta es $12.58. El impuesto de venta es 7.5% del precio. ¿Cuánto pagarías por la camiseta?
- La tienda compra un casco por $19.00 y lo vende por $31.50. ¿Cuál fue el porcentaje del incremento de precio?
- La tienda le paga $14.25 por hora a los trabajadores más un 5.5% de comisión. Si uno de ellos trabaja 18 horas y vende $250 en mercancía, ¿cuál es el monto total de su cheque de pago en este caso? Explica o muestra tu razonamiento.