Lección 2Ángulos adyacentes
Observemos algunas parejas especiales de ángulos.
Metas de aprendizaje:
- Puedo encontrar las medidas de ángulos desconocidos razonando sobre ángulos complementarios o suplementarios.
- Puedo reconocer cuando los ángulos adyacentes son complementarios o suplementarios.
2.1 Estimemos medidas de ángulos
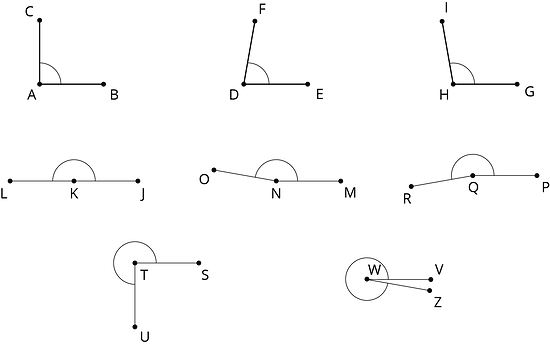
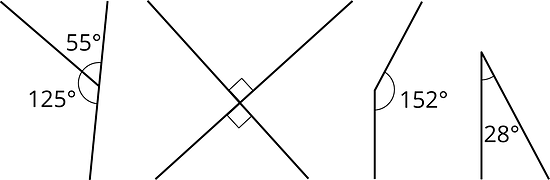
Haz una estimación de la medida en grados de cada uno de los ángulos señalados.
2.2 Recortemos rectángulos
Tu profesor te dará dos hojas pequeñas rectangulares.
- En una de las hojas, dibuja medio círculo en la mitad de un borde.

- Corta por una línea recta, empezando desde el centro del medio círculo hasta el otro lado del papel para obtener 2 pedazos distintos de papel (el corte no debe ser perpendicular al borde del papel).
- En cada uno de estos pedazos, mide el ángulo que está señalado por una parte de un círculo. Etiqueta la medida del ángulo en este pedazo de papel.
- ¿Qué observas sobre las medidas de estos ángulos?
- Clare midió 70 grados en uno de sus pedazos. Predice la medida del ángulo en su otro pedazo de papel.
- En el otro papel rectangular, dibuja un pequeño cuarto de círculo en una de las esquinas.
- Repite los pasos anteriores para cortar, medir y etiquetar los dos ángulos señalados por una parte de un círculo.

- ¿Qué observas sobre las medidas de estos ángulos?
- Priya midió 53 grados en uno de sus pedazos. Predice la medida del ángulo en su otro pedazo de papel.
2.3 ¿Es un complemento o un suplemento?
-
Usa el transportador de la imagen para encontrar la medida de los ángulos:
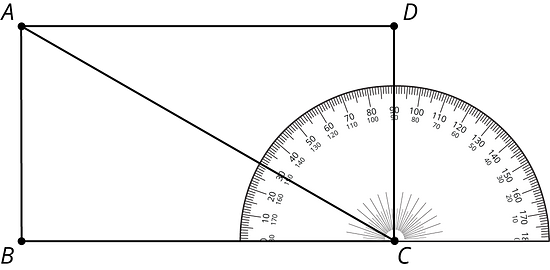
-
Explica cómo encontrar la medida del ángulo sin reubicar el transportador.
-
Usa el transportador de la imagen para encontrar la medida de los ángulos:

-
Explica cómo encontrar la medida del ángulo sin reubicar el transportador.
- El ángulo es un ángulo recto. Encuentra la medida del ángulo .

- El punto está sobre la recta . Encuentra la medida del ángulo .
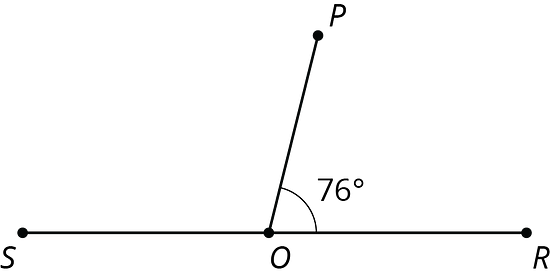
¿Estás listo para más?
Clare empezó con un pedazo de papel rectangular. Hizo un doblez en una esquina y luego dobló la otra esquina, como se muestra en las fotos.



- Intenta hacerlo tú mismo con un pedazo de papel rectangular. Dobla la esquina izquierda en cualquier ángulo y luego dobla la esquina derecha para que los bordes del papel se encuentren.
- Clare pensó que el ángulo de abajo parecía un ángulo de 90 grados. ¿El tuyo también parece ser de 90 grados?
- ¿Puedes explicar por qué el ángulo de abajo siempre tiene que ser 90 grados? Pista: la tercera foto muestra el papel de Clare desdoblado. Las marcas de los pliegues tienen líneas punteadas y la línea donde se tocaban los dos bordes de la hoja tiene una línea continua. Haz estas marcas en tu hoja.
Resumen de la lección 2
Si las medidas de dos ángulos suman , entonces decimos que los ángulos son complementarios. Estos son tres ejemplos de parejas de ángulos complementarios.
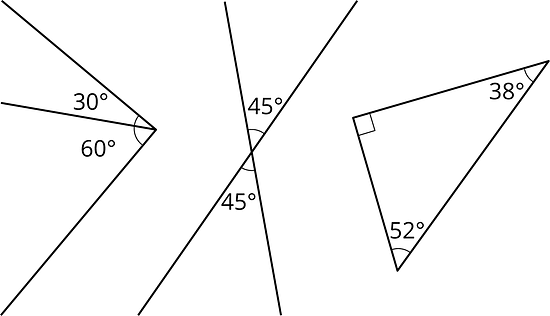
Si las medidas de dos ángulos suman , entonces decimos que los ángulos son suplementarios. Estos son tres ejemplos de parejas de ángulos suplementarios.
Términos del glosario
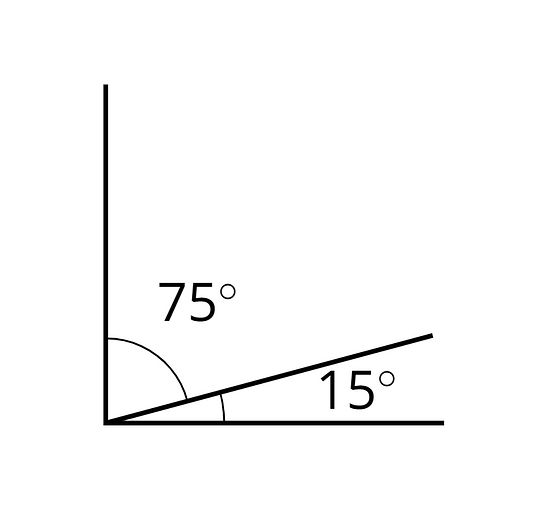
Dos ángulos son complementarios si sus medidas suman 90 grados.
Por ejemplo, un ángulo de y un ángulo de son complementarios.
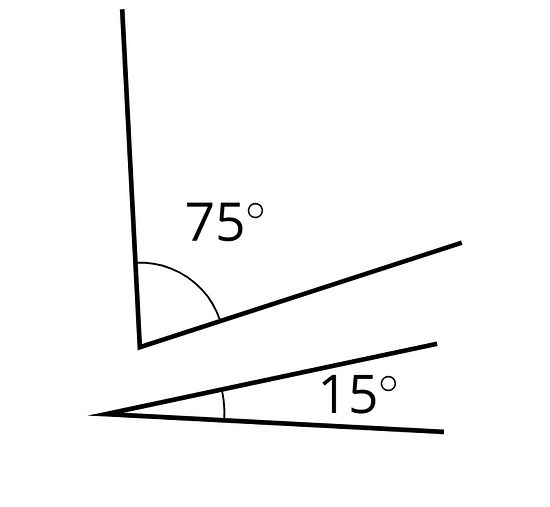
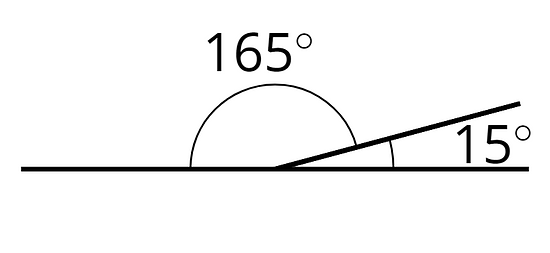
Dos ángulos son suplementarios si sus medidas suman 180 grados.
Por ejemplo, un ángulo de y un ángulo de son suplementarios.
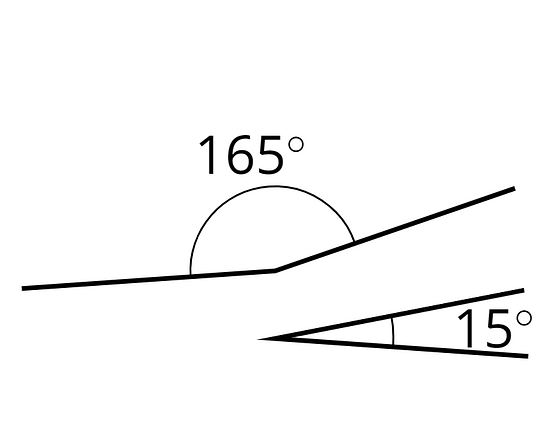
Problemas de práctica de la lección 2
Los ángulos y son suplementarios. Encuentra la medida del ángulo .
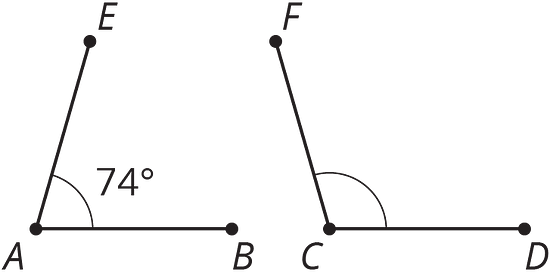
-
Encuentra dos parejas de ángulos en el cuadrado que sean complementarios.
- Encuentra tres ángulos cuya suma sea .
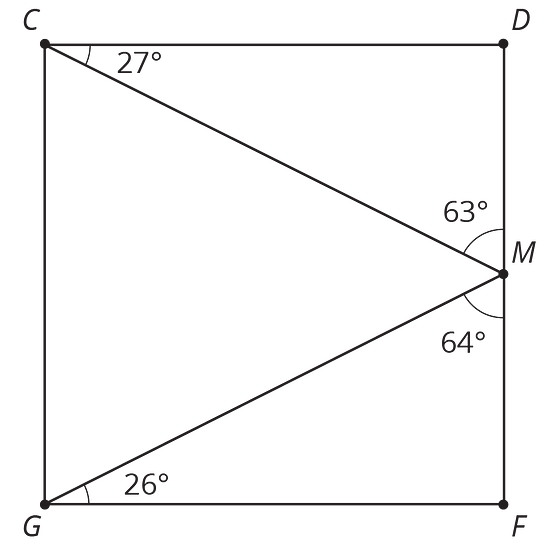
-
Completa la ecuación con un número que haga que la expresión del lado derecho del igual sea equivalente a la expresión del lado izquierdo.
Empareja cada tabla con la ecuación que representa la misma relación proporcional.
-
2 8 3 12 4 16 5 20 -
3 4.5 6 9 7 10.5 10 15 -
2 4 5 6 12 15
-