Open Up Resources Logo

Lección 5Usemos ecuaciones para encontrar ángulos desconocidos

Encontremos ángulos desconocidos usando ecuaciones.

Metas de aprendizaje:

  • Puedo escribir una ecuación para representar una relación entre medidas de ángulos y resolver la ecuación para encontrar las medidas de los ángulos desconocidos.

5.1 ¿Es suficiente?

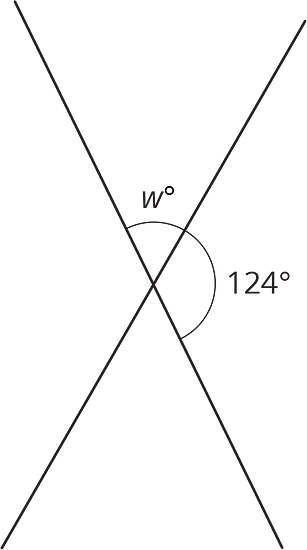
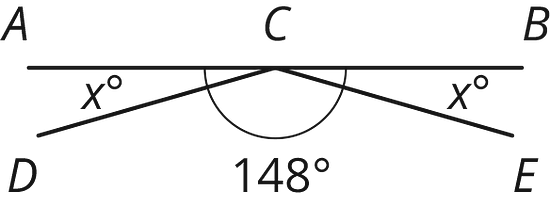
Tyler piensa que en esta figura hay suficiente información para descifrar los valores de a y  b .

¿Estás de acuerdo? Explica tu razonamiento.

5.2 ¿A qué se parece?

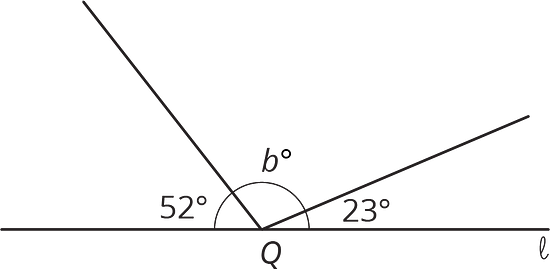
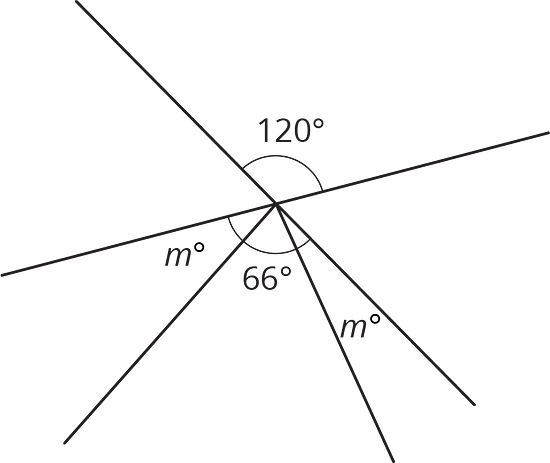
Elena y Diego escribieron cada uno ecuaciones para representar estos diagramas. Para cada diagrama, decide con cuál ecuación estás de acuerdo y resuélvela. Puedes suponer que los ángulos que parecen ángulos rectos en efecto son ángulos rectos.

  1. Elena: x=35
    Diego: x+35=180
  1. Elena: 35+w+41=180
    Diego: 35+w=180
  1. Elena:  w + 35 = 90
    Diego: 2w+35=90
  1. Elena: 2w + 35 = 90
    Diego: w+35=90
  1. Elena: w + 148 = 180
    Diego: x+90=148

5.3 Calculemos la medida

Encuentra las medidas de los ángulos desconocidos. Muestra tu razonamiento. Organízalo de tal forma que otras personas lo puedan entender.



  1. Las rectas \ell y  m son perpendiculares.

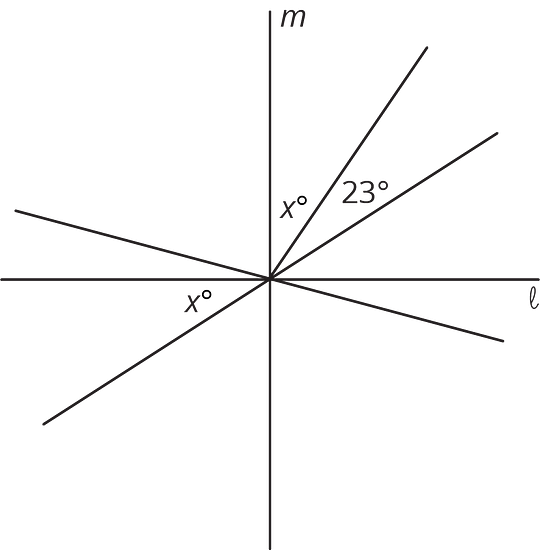
¿Estás listo para más?

El diagrama tiene tres cuadrados. Se han dibujado tres rectas adicionales que unen las esquinas de los cuadrados. Queremos encontrar el valor exacto de  a+b+c .

  1. Usa un transportador para medir los tres ángulos. Usa tus mediciones para estimar el valor de  a+b+c .
  2. Encuentra el valor exacto de  a+b+c razonando acerca del diagrama.

Resumen de la lección 5

Para encontrar una medida desconocida de un ángulo, algunas veces es útil escribir y resolver una ecuación que representa la situación. Por ejemplo, supongamos que queremos saber el valor de x en este diagrama.

Usando lo que sabemos sobre ángulos opuestos por el vértice, podemos escribir la ecuación  3x + 90 = 144 para representar esta situación. Luego podemos resolver la ecuación.

\begin{align} 3x + 90 &= 144 \\ 3x + 90 - 90 &= 144 - 90 \\ 3x &= 54 \\ 3x \boldcdot \frac13 &= 54 \boldcdot \frac13 \\ x &= 18 \end{align}

Problemas de práctica de la lección 5

  1. Las rectas  AB , DC y  EC se intersecan en el punto C . El ángulo  DCE mide 148^\circ . Encuentra el valor  x .

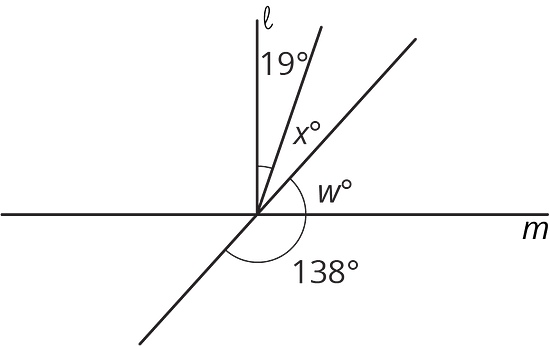
  2. La recta  \ell es perpendicular a la recta  m . Encuentra el valor de  x y  w .

  3. Si sabes que dos ángulos son complementarios y te dan la medida de uno de los ángulos, ¿puedes encontrar la medida del otro ángulo? Explica tu razonamiento.

  4. Para cada desigualdad, decide si la solución está representada por x < 4.5 o  x > 4.5 .

    1. \text-24>\text-6(x-0.5)
    2. \text-8x + 6 > \text-30
    3. \text-2(x + 3.2) < \text-15.4

  5. Un corredor corrió \frac23 de una carrera de 5 kilómetros en 21 minutos. Él corrió toda la carrera a una velocidad constante. 

    1. ¿Cuánto tiempo le tomó correr toda la carrera?
    2. ¿Cuánto tiempo le tomó correr 1 kilómetro? 

  6. Jada, Elena, y Lin caminaron 37 millas en total la última semana. Jada caminó 4 millas más que Elena, y Lin caminó 2 millas más que Jada. El diagrama representa esta situación:

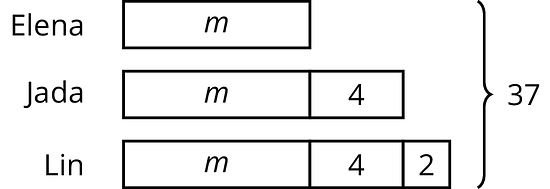
    Three tape diagrams are labeled “Elena”, “Jada,” and “Lin.” Elena’s tape diagram is of 1 part labeled m. Jada’s tape diagram is partitioned into 2 parts labeled m and 4. Lin’s tape diagram is partitioned into 3 parts labeled m, 4, and 2. A brace is drawn that contains of all 3 diagrams and is labeled 37.

    Encuentra el número de millas que cada uno caminó. Explica o muestra tu razonamiento.

  7. Selecciona todas las expresiones que sean equivalentes a  \text-36x+54y-90 .

    1. \text-9(4x-6y-10)
    2. \text-18(2x-3y+5)
    3. \text-6(6x+9y-15)
    4. 18(\text-2x+3y-5)
    5. \text-2(18x-27y+45)
    6. 2(\text-18x+54y-90)