Lección 14Usemos relaciones lineales para resolver problemas
Escribamos ecuaciones para situaciones de la vida real y pensemos acerca de sus soluciones.
Metas de aprendizaje:
- Puedo escribir ecuaciones lineales para razonar acerca de situaciones de la vida real.
14.1 Compremos frutas
Para cada relación descrita, escribe una ecuación que represente la relación.
- Las uvas cuestan $2.39 por cada libra. Los bananos cuestan $0.59 por cada libra. Tienes $15 para gastar en libras de uvas y libras de bananos.
- En una cuenta de ahorros hay $50 al comienzo del año y se depositan $20 cada semana. Después de semanas, hay dólares en la cuenta.
14.2 Cinco cuentas de ahorros
Cada recta representa el saldo semanal de la cuenta de ahorros de una persona desde el comienzo del año.
- Escoge una recta y escribe una descripción de lo que ocurre con la cuenta de esa persona durante las primeras 17 semanas del año. No le digas a tu grupo cuál recta escogiste.
- Comparte tu historia con tu grupo y mira si alguien puede adivinar cuál es tu recta.
- Escribe una ecuación para cada una de las rectas que están en la gráfica. ¿Qué significan la pendiente, , y la intersección con el eje vertical, , en la situación?
- ¿Para cuál ecuación es una solución? Interpreta esta solución en términos de tu historia.
- Predice cuál será el saldo de cada cuenta después de 20 semanas.
14.3 Pescados fabulosos
El supermercado "Pescados fabulosos" pide tilapia, que cuesta $3 por cada libra, y salmón, que cuesta $5 por cada libra. El supermercado tiene un presupuesto de $210 para gastar en este pedido cada día.
- Escribe cinco combinaciones diferentes de salmón y tilapia que puede pedir el supermercado.
- Define las variables y escribe una ecuación que represente la relación que hay entre la cantidad de cada pescado comprada y cuánto dinero gasta el supermercado.
- Dibuja una gráfica de la relación. Etiqueta tus ejes.
- Sobre tu gráfica, ubica y etiqueta las combinaciones de la A a la F.
A B C D E F libras de tilapia 5 19 27 25 65 55 libras de salmón 36 30.6 25 27 6 4 - ¿Cuáles de estas combinaciones puede pedir el supermercado? Explica o muestra tu razonamiento.
- Menciona dos maneras en las que puedas saber si un par de números es una solución de una ecuación.
Problemas de práctica de la lección 14
El dueño de un nuevo restaurante está pidiendo mesas y sillas. Él quiere tener únicamente mesas para 2 y mesas para 4. El número total de personas que se pueden sentar en el restaurante es 120.
- Describe algunas combinaciones posibles de mesas de 2 puestos y mesas de 4 puestos en las que se puedan sentar los 120 clientes. Explica cómo las hallaste.
- Escribe una ecuación que represente la situación. ¿Qué representan las variables?
- Elabora una gráfica que represente la situación.
- ¿Qué nos dice la pendiente sobre la situación?
- Interpreta las intersecciones con el eje y con el eje en la situación.
El triángulo es isósceles y tiene dos ángulos de medida grados y un ángulo de medida grados.
- Halla tres combinaciones de y que hagan verdadera esta frase.
- Escribe una ecuación que relacione a y a .
- Si tuvieras que dibujar la gráfica de esta ecuación lineal, ¿cuál sería su pendiente? ¿Cómo podrías interpretar la pendiente en el contexto del triángulo?
Selecciona todas las ecuaciones para las que es una solución.
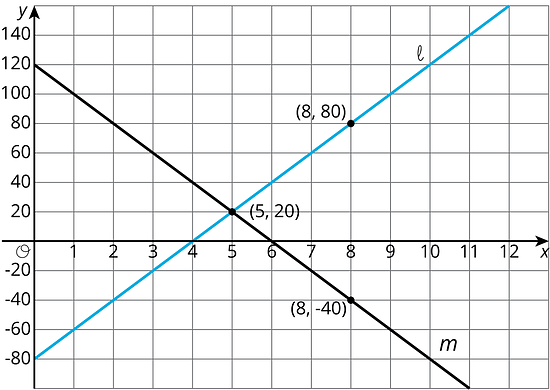
Considera las siguientes gráficas de ecuaciones lineales. Decide cuál recta tiene una pendiente positiva y cuál tiene una pendiente negativa. Luego calcula la pendiente exacta de cada recta.