Lección 12¿Cuánto cabe?
Razonemos sobre el volumen de diferentes figuras.
Metas de aprendizaje:
- Reconozco las figuras tridimensionales: cilindro, cono, prisma rectangular y esfera.
- Sé que el volumen es la cantidad de espacio contenido dentro de una figura de tridimensional.
12.1 Dos recipientes
Tu profesor les mostrará algunos recipientes. El recipiente pequeño tiene 200 frijoles. Estimen cuántos frijoles contiene el tarro grande.
12.2 ¿Cuál es tu estimación?
Tu profesor les mostrará algunos recipientes.
- Si la caja de pasta contiene 8 tazas de arroz, ¿cuánto arroz necesitarías para llenar los otros prismas rectangulares?
- Si la calabaza puede contener 15 onzas líquidas de arroz, ¿cuánto contienen los otros cilindros?
- Si el cono pequeño contiene 2 onzas líquidas de arroz, ¿cuánto contiene el cono grande?
- Si la bola de golf estuviera hueca, contendría alrededor de 0.2 tazas de agua. Si la pelota de béisbol estuviera hueca, ¿cuánto contendría la esfera?
12.3 ¿Conoces estas figuras?
- ¿De qué formas son las caras de cada tipo de objeto que se muestra aquí? Por ejemplo, todas las seis caras de un cubo son cuadrados.

- ¿Cuáles caras se podrían considerar como una "base" del objeto?
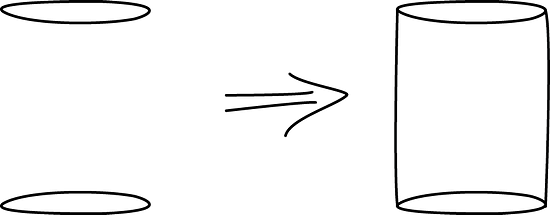
- Este es un método para dibujar rápidamente un cilindro:
- Dibuja dos óvalos.
- Une las aristas.
- ¿Cuáles partes de tu dibujo estarían ocultas detrás del cilindro? Haz estas partes con líneas punteadas.
¿Estás listo para más?
Una pelota de fútbol es un poliedro con 12 caras pentagonales negras y 20 caras hexagonales blancas. ¿Cuántas aristas hay en total en este poliedro?

Resumen de la lección 12
El volumen de una figura tridimensional, como un tarro o una habitación, es la cantidad de espacio que la figura encierra. Se puede medir el volumen al determinar el número de unidades de volumen de igual tamaño que llenan la figura sin dejar huecos o sin superposiciones. Por ejemplo, se podría decir que una habitación tiene un volumen de 1,000 pies cúbicos, o que una jarra puede tener 5 galones de agua. Incluso se puede medir el volumen de un tarro con el número de frijoles que este podría contener, aunque el conteo de frijol en realidad no es una medida del volumen en el mismo modo que un centímetro cúbico lo es porque hay espacio entre los frijoles. (El número de frijoles que caben en el tarro depende del volumen del tarro, así que esta "medida" está bien para estimar cuando se estén analizando los tamaños relativos de los recipientes).
En grados anteriores, se estudiaron figuras tridimensionales con caras planas que son polígonos. Se aprendió cómo calcular el volumen de prismas rectangulares. Ahora se estudiarán figuras tridimensionales con caras circulares y superficies curvas: conos, cilindros y esferas.
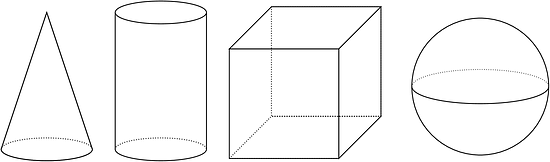
Para ayudar a ver mejor las figuras, se pueden usar líneas punteadas para representar partes que no sería posible ver si un objeto físico sólido estuviera en frente de uno. Por ejemplo, si se piensa que el cilindro en esta imagen representa una lata, el arco punteado en la mitad de la parte inferior de ese cilindro representa la mitad de atrás de la base circular de la lata. ¿Qué objetos podrían representar las otras figuras en la imagen?
Problemas de práctica de la lección 12
- Esboza un cubo y etiqueta su longitud de lado como 4 cm (este sería el cubo A).
- Esboza un cubo con lados que sean el doble de largo que el cubo A y etiqueta su longitud de lado (este sería el cubo B).
- Determina los volúmenes del cubo A y cubo B.
Varios acuarios de vidrio de distintos tamaños están para la venta en una tienda de mascotas. Todos tienen forma de prismas rectangulares. Un tanque de 15 galones tiene 24 pulgadas de largo, 12 pulgadas de ancho y 12 pulgadas de alto. Empareja las dimensiones de los otros tanques con el volumen de agua que cada uno de ellos puede contener.
- Tanque 1: 36 pulgadas de largo, 18 pulgadas de largo y 12 pulgadas de alto
- Tanque 2: 16 pulgadas de largo, 8 pulgadas de largo y 10 pulgadas de alto
- Tanque 3: 30 pulgadas de largo, 12 pulgadas de largo y 12 pulgadas de alto
- Tanque 4: 20 pulgadas de largo, 10 pulgadas de largo y 12 pulgadas de alto
- 5 galones
- 10 galones
- 20 galones
- 30 galones
Dos vasos de papel tienen la forma de conos. El cono pequeño puede contener 6 oz de agua. El cono grande es de la altura y del diámetro del cono pequeño. ¿Cuál de estas podría ser la cantidad de agua que contiene el cono grande?
- 8 cm
- 14 oz
- 4.5 oz
- 14 cm
La gráfica representa el volumen de un cilindro que tiene una altura igual a su radio.
- Si el diámetro es 2, ¿cuál es el radio del cilindro?
- Expresa el volumen de un cubo de longitud de lado como una ecuación.
- Realiza una tabla para el volumen del cubo con , , y .
- ¿Cuál volumen es mayor: el del cubo, si , o el del cilindro, si su diámetro es 3?
Selecciona todos los puntos que están sobre una recta que tiene pendiente 2 y que también contiene al punto .
Resuelve: