Lesson 6Methods for Multiplying Decimals
Let’s look at some ways we can represent multiplication of decimals.
Learning Targets:
- I can use area diagrams to represent and reason about multiplication of decimals.
- I know and can explain more than one way to multiply decimals using fractions and place value.
6.1 Which One Doesn’t Belong: Products
Which expression doesn’t belong? Explain your reasoning.
A.
B.
C.
D.
6.2 Using Properties of Numbers to Reason about Multiplication
- Elena and Noah used different methods to compute . Both computations were correct.
Analyze the two methods, then discuss these questions with your partner.
- Which method makes more sense to you? Why?
- What might Elena do to compute ? What might Noah do to compute ? Will the two methods result in the same value?
-
Compute each product using the equation and what you know about fractions, decimals, and place value. Explain or show your reasoning.
6.3 Using Area Diagrams to Reason about Multiplication
-
In the diagram, the side length of each square is 0.1 unit.
- Explain why the area of each square is not 0.1 square unit.

- How can you use the area of each square to find the area of the rectangle? Explain or show your reasoning.
- Explain how the diagram shows that the equation is true.
-
Label the squares with their side lengths so the area of this rectangle represents .
- What is the area of each square?
- Use the squares to help you find . Explain or show your reasoning.

- Label the squares with their side lengths so the area of this rectangle represents .
Next, use the diagram to help you find . Explain or show your reasoning.

Lesson 6 Summary
Here are three other ways to calculate a product of two decimals such as .
-
First, we can multiply each decimal by the same power of 10 to obtain whole-number factors.
Because we multiplied both 0.04 and 0.07 by 100 to get 4 and 7, the product 28 is times the original product, so we need to divide 28 by 10,000.
- Second, we can write each decimal as a fraction, and , and multiply them.
-
Third, we can use an area model. The product can be thought of as the area of a rectangle with side lengths of 0.04 unit and 0.07 unit.

In this diagram, each small square is 0.01 unit by 0.01 unit. Its area, in square units, is therefore , which is .
Because the rectangle is composed of 28 small squares, its area, in square units, must be:
All three calculations show that .
Lesson 6 Practice Problems
Find each product. Show your reasoning.
You can use a rectangle to represent .
- What must the side length of each square represent for the rectangle to correctly represent ?
- What area is represented by each square?
- What is ? Show your reasoning.

One gallon of gasoline in Buffalo, New York costs $2.29. In Toronto, Canada, one liter of gasoline costs $0.91. There are 3.8 liters in one gallon.
- How much does one gallon of gas cost in Toronto? Round your answer to the nearest cent.
- Is the cost of gas greater in Buffalo or in Toronto? How much greater?
- Calculate each sum or difference.
Find the value of using any method.
Find the area of the shaded region. All angles are right angles. Show your reasoning.
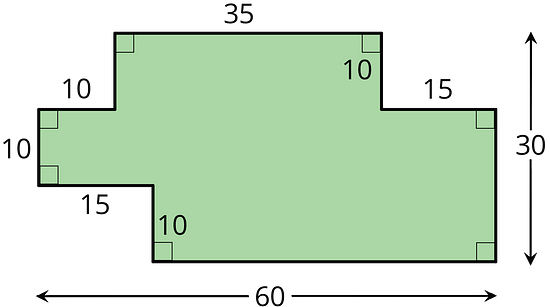
- Priya finds by calculating , then moving the decimal point three places to the left. Why does Priya’s method make sense?
- Use Priya’s method to calculate . You can use the fact that .
- Use Priya’s method to calculate .