Lesson 10Finding and Interpreting the Mean as the Balance Point
Let's look at another way to understand the mean of a data set.
Learning Targets:
- I can describe what the mean tells us in the context of the data.
- I can explain how the mean represents a balance point for the data on a dot plot.
10.1 Which One Doesn’t Belong: Division
Which expression does not belong? Be prepared to explain your reasoning.
10.2 Travel Times (Part 1)
Here is the data set from an earlier lesson showing how long it takes for Diego to walk to school, in minutes, over 5 days. The mean number of minutes was 11.
- Represent Diego’s data on a dot plot. Mark the location of the mean with a triangle ().
| 12 | 7 | 13 | 9 | 14 |
-
The mean can also be seen a measure of center that balances the points in a data set. If we find the distance between every point and the mean, add the distances on each side of the mean, and compare the two sums, we can see this balancing.
-
Record the distance between each point and 11 and its location relative to 11.
time in minutes distance from 11 left of 11 or right of 11? 12 7 13 9 14 -
Sum of distances left of 11:___________ Sum of distances right of 11:___________
What do you notice about the two sums?
-
- Can another point that is not the mean produce similar sums of distances?
Let’s investigate whether 10 can produce similar sums as those of 11.
- Complete the table with the distance of each data point from 10.
time in minutes distance from 10 left of 10 or right of 10? 12 7 13 9 14 -
Sum of distances left of 10:___________ Sum of distances right of 10:___________
What do you notice about the two sums?
- Complete the table with the distance of each data point from 10.
- Based on your work so far, explain why the mean can be considered a balance point for the data set.
10.3 Travel Times (Part 2)
-
Here are dot plots showing how long Diego’s trips to school took in minutes—which you studied earlier—and how long Andre’s trips to school took in minutes. The dot plots include the means for each data set, marked by triangles.
- Which of the two data sets has a larger mean? In this context, what does a larger mean tell us?
- Which of the two data sets has larger sums of distances to the left and right of the mean? What do these sums tell us about the variability in Diego’s and Andre’s travel times?
-
Here is a dot plot showing lengths of Lin’s trips to school.
- Calculate the mean of Lin’s travel times.
- Complete the table with the distance between each point and the mean as well as whether the point is to the left or right of the mean.
time in minutes distance from the mean left or right of the mean? 22 18 11 8 11 - Find the sum of distances to the left of the mean and the sum of distances to the right of the mean.
- Use your work to compare Lin’s travel times to Andre’s. What can you say about their average travel times? What about the variability in their travel times?
Lesson 10 Summary
Why is this a good way to think about the mean? Let’s look at a very simple set of data on the number of cookies that each of eight friends baked, shown in the table and dot plot.
| 19 | 20 | 20 | 21 | 21 | 22 | 22 | 23 |
The distribution shown is completely symmetrical. The mean number of cookies is 21, because . If we mark the location of the mean on the dot plot, we can see that the data points could balance at 21.
In this plot, each point on either side of the mean has a mirror image. For example, the two points at 20 and the two at 22 are the same distance from 21, but each pair is located on either side of 21. We can think of them as balancing each other around 21.
Similarly, the points at 19 and 23 are the same distance from 21 but are on either side of it. They, too, can be seen as balancing each other around 21.
We can say that the distribution of the cookies has a center at 21 because that is its balance point, and that the eight friends, on average, baked 21 cookies.
Even when a distribution is not completely symmetrical, the distances of values below the mean, on the whole, balance the distances of values above the mean.
Glossary Terms
A measure of center is a value that seems typical for a data distribution.
Mean and median are both measures of center.
Lesson 10 Practice Problems
On school days, Kiran walks to school. Here are the lengths of time, in minutes, for Kiran’s walks on 5 school days.
- Create a dot plot for Kiran’s data.
16 11 18 12 13 - Without calculating, decide if 15 minutes would be a good estimate of the mean. If you think it is a good estimate, explain your reasoning. If not, give a better estimate and explain your reasoning.
- Calculate the mean for Kiran’s data.
- In the table, record the distance of each data point from the mean and its location relative to the mean.
time in minutes distance from the mean left or right of the mean? 16 11 18 12 13 - Calculate the sum of all distances to the left of the mean, then calculate the sum of distances to the right of the mean. Explain how these sums show that the mean is a balance point for the values in the data set.
Noah scored 20 points in a game. Mai's score was 30 points. The mean score for Noah, Mai, and Clare was 40 points. What was Clare's score? Explain or show your reasoning.
Compare the numbers using >, <, or =.
- _____
- _____
- _____
- _____
- _____
- _____
-
Plot and on a number line.
- Is , or is ? Explain how you know.
-
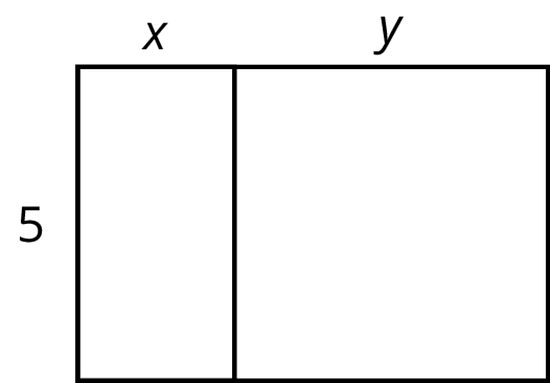
Select all expressions that represent the total area of the large rectangle.