Lesson 6Estimating Areas
Let’s estimate the areas of weird shapes.
Learning Targets:
- I can calculate the area of a complicated shape by breaking it into shapes whose area I know how to calculate.
6.1 Mental Calculations
Find a strategy to make each calculation mentally:
6.2 House Floorplan
Here is a floor plan of a house. Approximate lengths of the walls are given.
6.3 Area of Nevada
Estimate the area of Nevada in square miles. Explain or show your reasoning.

Are you ready for more?
The two triangles are equilateral, and the three pink regions are identical. The blue equilateral triangle has the same area as the three pink regions taken together. What is the ratio of the sides of the two equilateral triangles?

Lesson 6 Summary
We can find the area of some complex polygons by surrounding them with a simple polygon like a rectangle. For example, this octagon is contained in a rectangle.

We can estimate the area of irregular shapes by approximating them with a polygon and finding the area of the polygon. For example, here is a satellite picture of Lake Tahoe with some one-dimensional measurements around the lake.

Lesson 6 Practice Problems
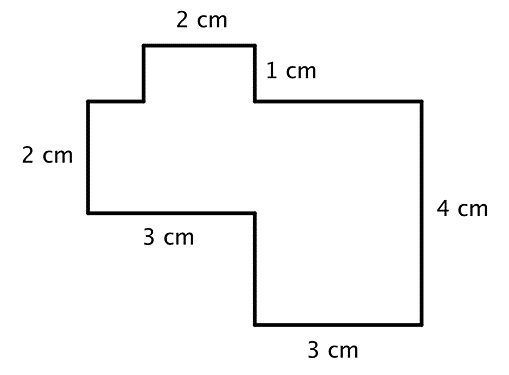
Find the area of the polygon.
- Draw polygons on the map that could be used to approximate the area of Virginia.
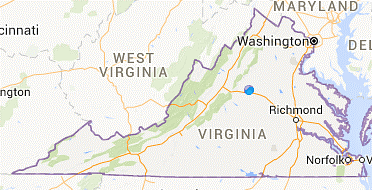
“Map of Virginia” by United States Census Bureau via American Fact Finder. Public Domain. - Which measurements would you need to know in order to calculate an approximation of the area of Virginia? Label the sides of the polygons whose measurements you would need. (Note: You aren’t being asked to calculate anything.)
- Draw polygons on the map that could be used to approximate the area of Virginia.
Jada’s bike wheels have a diameter of 20 inches. How far does she travel if the wheels rotate 37 times?
The radius of the earth is approximately 6400 km. The equator is the circle around the earth dividing it into the northern and southern hemisphere. (The center of the earth is also the center of the equator.) What is the length of the equator?
Here are several recipes for sparkling lemonade. For each recipe describe how many tablespoons of lemonade mix it takes per cup of sparkling water.
Recipe 1: 4 tablespoons lemonade mix and 12 cups of sparkling water
Recipe 2: 4 tablespoons of lemonade mix and 6 cups of sparkling water
Recipe 3: 3 tablespoons of lemonade mix and 5 cups of sparkling water
Recipe 4: tablespoon os lemonade mix and cups of sparkling water