Lesson 7Exploring the Area of a Circle
Let’s investigate the areas of circles.
Learning Targets:
- I know whether or not the relationship between the diameter and area of a circle is proportional and can explain how I know.
- If I know a circle’s radius or diameter, I can find an approximation for its area.
7.1 Estimating Areas
7.2 Estimating Areas of Circles
Your teacher will assign your group two circles of different sizes.
- Set the diameter of your assigned circle and use the applet to help estimate the area of the circle.
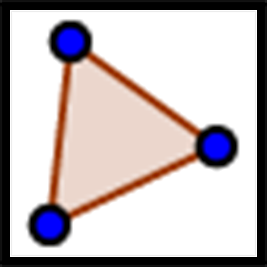
Note: to create a polygon, select the Polygon tool, and click on each vertex. End by clicking the first vertex again. For example, to draw triangle , click on ---.
- Record the diameter in column and the corresponding area in column for your circles and others from your classmates.
-
In a previous lesson, you graphed the relationship between the diameter and circumference of a circle. How is this graph the same? How is it different?
Are you ready for more?
- How many circles of radius 1 unit can you fit inside a circle of radius 2 units so that they do not overlap?
- How many circles of radius 1 unit can you fit inside a circle of radius 3 units so that they do not overlap?
- How many circles of radius 1 unit can you fit inside a circle of radius 4 units so that they do not overlap?
If you get stuck, consider using coins or other circular objects.
7.3 Covering a Circle
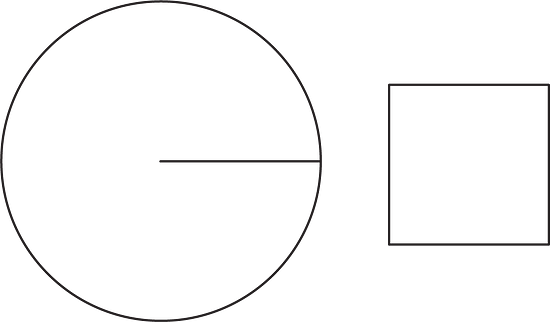
Here is a square whose side length is the same as the radius of the circle.
Lesson 7 Summary
The circumference of a circle is proportional to the diameter , and we can write this relationship as . The circumference is also proportional to the radius of the circle, and the constant of proportionality is because the diameter is twice as long as the radius. However, the area of a circle is not proportional to the diameter (or the radius).
The area of a circle with radius is a little more than 3 times the area of a square with side so the area of a circle of radius is approximately . We saw earlier that the circumference of a circle of radius is . If we write for the circumference of a circle, this proportional relationship can be written .
The area of a circle with radius is approximately . Unlike the circumference, the area is not proportional to the radius because cannot be written in the form for a number . We will investigate and refine the relationship between the area and the radius of a circle in future lessons.
Glossary Terms
The area of a circle whose radius is units is square units.
A circle has radius 3 inches. Its area is square inches, which is approximately 28.3 square inches.
Lesson 7 Practice Problems
The -axis of each graph has the diameter of a circle in meters. Label the -axis on each graph with the appropriate measurement of a circle: radius (m), circumference (m), or area (m2).
-
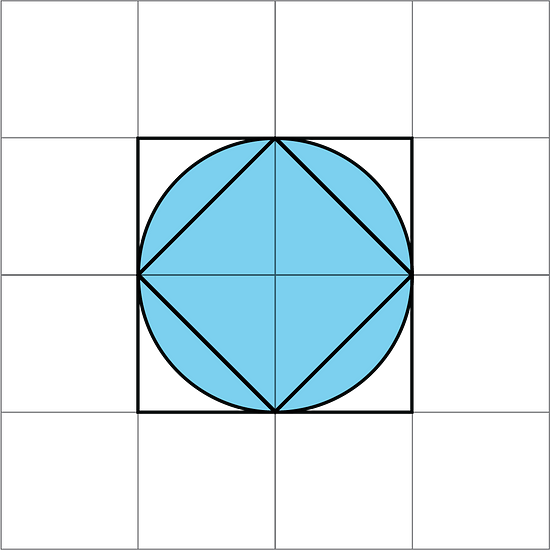
Here is a picture of two squares and a circle. Use the picture to explain why the area of this circle is more than 2 square units but less than 4 square units.
-
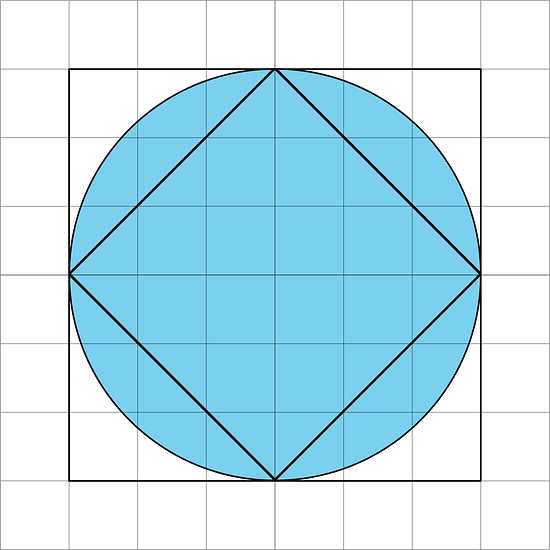
Here is another picture of two squares and a circle. Use the picture to explain why the area of this circle is more than 18 square units and less than 36 square units.
-
Circle A has area 500 in2. The diameter of circle B is three times the diameter of circle A. Estimate the area of circle B.
Lin’s bike travels 100 meters when her wheels rotate 55 times. What is the circumference of her wheels?
Find the circumference of this circle.
Priya drew a circle whose circumference is 25 cm. Clare drew a circle whose diameter is 3 times the diameter of Priya’s circle. What is the circumference of Clare’s circle?