Lesson 4Half as Much Again
Let’s use fractions to describe increases and decreases.
Learning Targets:
- I can use the distributive property to rewrite an expression like as .
- I understand that “half as much again” and “multiply by ” mean the same thing.
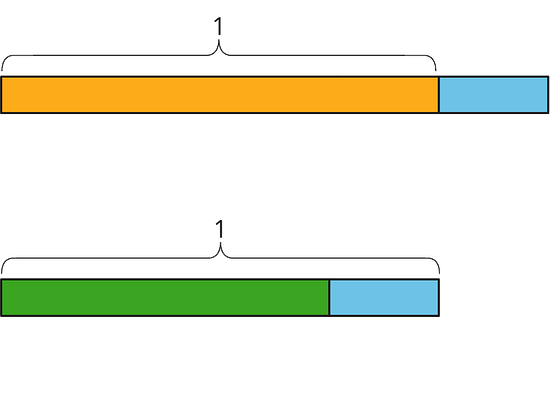
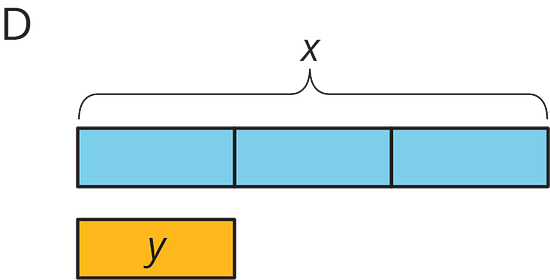
4.1 Notice and Wonder: Tape Diagrams
What do you notice? What do you wonder?
4.2 Walking Half as Much Again
-
Complete the table to show the total distance walked in each case.
- Jada’s pet turtle walked 10 feet, and then half that length again.
- Jada’s baby brother walked 3 yards, and then half that length again.
- Jada’s hamster walked 4.5 km, and then half that length again.
- Jada’s robot walked 1 mile, and then half that length again.
- A person walked meters and then half that length again.
initial distance total distance 10 3 4.5 1 - Explain how you computed the total distance in each case.
-
Two students each wrote an equation to represent the relationship between the initial distance walked () and the total distance walked ().
- Mai wrote .
- Kiran wrote .
Do you agree with either of them? Explain your reasoning.
Are you ready for more?
Zeno jumped 8 meters. Then he jumped half as far again (4 meters). Then he jumped half as far again (2 meters). So after 3 jumps, he was meters from his starting place.
- Zeno kept jumping half as far again. How far would he be after 4 jumps? 5 jumps? 6 jumps?
- Before he started jumping, Zeno put a mark on the floor that was exactly 16 meters from his starting place. How close can Zeno get to the mark if he keeps jumping half as far again? (Consider researching Zeno's Paradox.)
4.3 More and Less
-
Match each situation with a diagram. A diagram may not have a match.
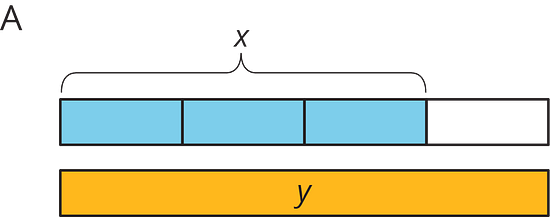
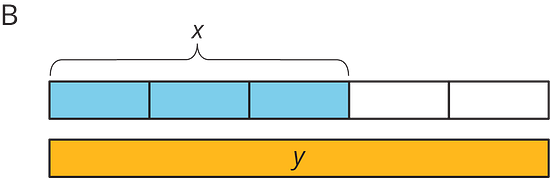
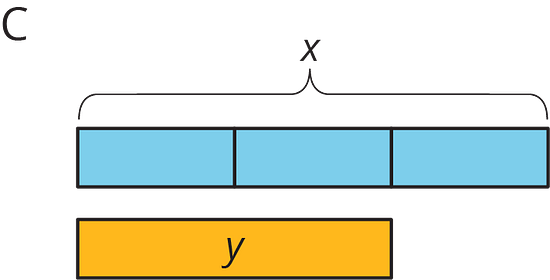
- Han ate ounces of blueberries. Mai ate less than that.
- Mai biked miles. Han biked more than that.
- Han bought pounds of apples. Mai bought of that.
- For each diagram, write an equation that represents the relationship between and .
- Diagram A:
- Diagram B:
- Diagram C:
- Diagram D:
- Write a story for one of the diagrams that doesn't have a match.
4.4 Card Sort: Representations of Proportional Relationships
Your teacher will give you a set of cards that have proportional relationships represented 3 different ways: as descriptions, equations, and tables. Mix up the cards and place them all face-up.
- Take turns with a partner to match a description with an equation and a table.
- For each match you find, explain to your partner how you know it’s a match.
- For each match your partner finds, listen carefully to their explanation, and if you disagree, explain your thinking.
- When you agree on all of the matches, check your answers with the answer key. If there are any errors, discuss why and revise your matches.
Lesson 4 Summary
Using the distributive property provides a shortcut for calculating the final amount in situations that involve adding or subtracting a fraction of the original amount.
For example, one day Clare runs 4 miles. The next day, she plans to run that same distance plus half as much again. How far does she plan to run the next day?
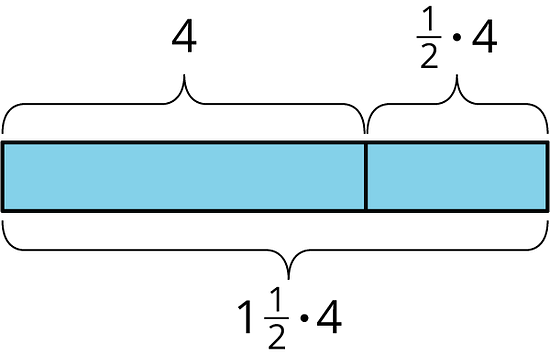
Tomorrow she will run 4 miles plus of 4 miles. We can use the distributive property to find this in one step:
Clare plans to run , or 6 miles.
This works when we decrease by a fraction, too. If Tyler spent dollars on a new shirt, and Noah spent less than Tyler, then Noah spent dollars since .
Lesson 4 Practice Problems
Match each situation with a diagram.
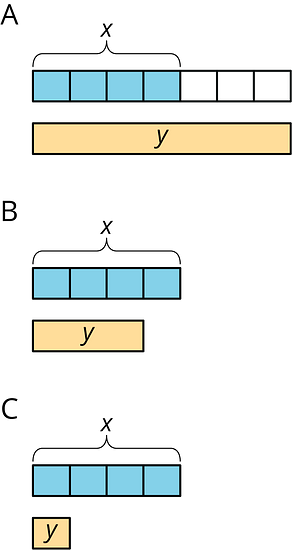
- Diego drank ounces of juice. Lin drank less than that.
- Lin ran miles. Diego ran more than that.
- Diego bought pounds of almonds. Lin bought of that.
Elena walked 12 miles. Then she walked that distance. How far did she walk all together? Select all that apply.
-
Write a story that can be represented by the equation .
Select all ratios that are equivalent to .
Jada is making circular birthday invitations for her friends. The diameter of the circle is 12 cm. She bought 180 cm of ribbon to glue around the edge of each invitation. How many invitations can she make?