Lesson 5Say It with Decimals
Let’s use decimals to describe increases and decreases.
Learning Targets:
- I can use the distributive property to rewrite an equation like .
- I can write fractions as decimals.
- I understand that “half as much again” and “multiply by 1.5” mean the same thing.
5.1 Notice and Wonder: Fractions to Decimals
A calculator gives the following decimal representations for some unit fractions:
What do you notice? What do you wonder?
5.2 Repeating Decimals
-
Use long division to express each fraction as a decimal.
- What is similar about your answers to the previous question? What is different?
- Use the decimal representations to decide which of these fractions has the greatest value. Explain your reasoning.
Are you ready for more?
5.3 More and Less with Decimals
-
Match each diagram with a description and an equation.
Diagrams:
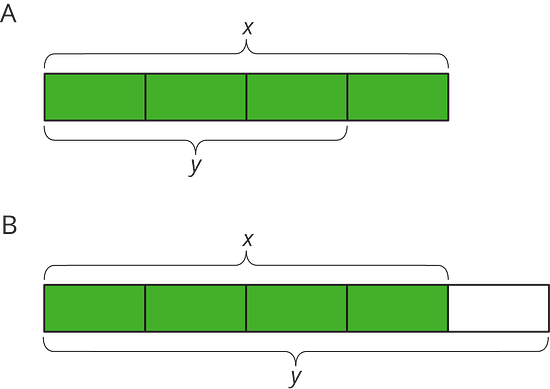
Descriptions:
An increase by
An increase by
An increase by
A decrease by
A decrease by
Equations:
- Draw a diagram for one of the unmatched equations.
5.4 Card Sort: More Representations
Your teacher will give you a set of cards that have proportional relationships represented 2 different ways: as descriptions and equations. Mix up the cards and place them all face-up.
Take turns with a partner to match a description with an equation.
- For each match you find, explain to your partner how you know it’s a match.
- For each match your partner finds, listen carefully to their explanation, and if you disagree, explain your thinking.
- When you have agreed on all of the matches, check your answers with the answer key. If there are any errors, discuss why and revise your matches.
Lesson 5 Summary
Long division gives us a way of finding decimal representations for fractions.
For example, to find a decimal representation for , we can divide 9 by 8.
So .
Sometimes it is easier to work with the decimal representation of a number, and sometimes it is easier to work with its fraction representation. It is important to be able to work with both. For example, consider the following pair of problems:
- Priya earned dollars doing chores, and Kiran earned as much as Priya. How much did Kiran earn?
- Priya earned dollars doing chores, and Kiran earned 1.2 times as much as Priya. How much did Kiran earn?
Since , these are both exactly the same problem, and the answer is or .
When we work with percentages in later lessons, the decimal representation will come in especially handy.
Glossary Terms
A repeating decimal has digits that keep going in the same pattern over and over. The repeating digits are marked with a line above them.
For example, the decimal representation for is , which means 0.3333333 . . . The decimal representation for is which means 1.136363636 . . .
Lesson 5 Practice Problems
- Match each diagram with a description and an equation.
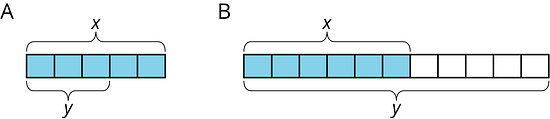
Descriptions:
An increase by
An increase by
A decrease by
A decrease by
Equations:
- Draw a diagram for one of the unmatched equations.
- Match each diagram with a description and an equation.
At the beginning of the month, there were 80 ounces of peanut butter in the pantry. Since then, the family ate 0.3 of the peanut butter. How many ounces of peanut butter are in the pantry now?
-
- On a hot day, a football team drank an entire 50-gallon cooler of water and half as much again. How much water did they drink?
- Jada has 12 library books checked out and Han has less than that. How many books does Han have checked out?
If represents a positive number, select all expressions whose value is greater than .
-
A person's resting heart rate is typically between 60 and 100 beats per minute. Noah looks at his watch, and counts 8 heartbeats in 10 seconds.
- Is his heart rate typical? Explain how you know.
- Write an equation for , the number of times Noah’s heart beats (at this rate) in minutes.